線形代数の基礎

機械学習の理論では線形代数で用いられる概念が多く登場します。 これらの概念を利用することで、複数の値や変数をまとめて扱うことができるようになり、数式を簡潔に表現できるようになります。 本章では、特に以下の概念を順番に紹介します

• スカラ・ベクトル・行列・テンソル

• ベクトル・行列の演算（加減算・スカラ倍・内積・行列積）

• 特別な行列（単位行列・逆行列）

• 多変数関数（線形結合，二次形式）とその微分

スカラ・ベクトル・行列・テンソル

まず始めに、スカラ、ベクトル、行列、テンソルという 4 つの言葉を解説します。

スカラ (scalar) は、2.5、-1、\(\sqrt{2}\)、\(\pi\)といった 1 つの値もしくは変数のことを指します。スカラは温度や身長といった単一の数量を表します。スカラ変数を表すには

\[x, \ y,\ M,\ N\]

のように、太字や斜体にされていない文字を利用するのが一般的です。 \(2.4+3.2i\)のような複素数でも、値が 1 つならばスカラ（複素数のスカラ）と呼びますが、本資料では特に明示しなければ実数のスカラを扱います。後述するベクトル、行列、テンソルについても同様です。

\(x\)が実数のスカラであることをしばしば「\(x\in \mathbb{R}\)」と書きます。 \(\mathbb{R}\) は実数のスカラからなる集合を表し、「\(A\in B\)」は「\(A\) は \(B\) に属する」という意味です。従って、\(x\in \mathbb{R}\) で「\(x\) は実数のスカラからなる集合に属する」、すなわち「\(x\) は実数のスカラである」と解釈できます。

ベクトル (vector) は、スカラを 1 方向に並べたものです。例えば、

\[\begin{split}{\bf x}=\begin{bmatrix} x_{1} \\ x_{2} \\ x_{3} \end{bmatrix}, \ {\bf y}=\begin{bmatrix} y_{1} \\ y_{2} \\ \vdots \\ y_{N} \end{bmatrix}\end{split}\]

のように表します。ベクトルを構成するスカラ達（\(x_1\) や \(y_2\) など）のことを要素や成分と呼びます。 ベクトルを表すのに用いられる文字は、スカラと区別しやすいよう太字とするのが一般的です。 上の 2 つの例のように、その要素を縦方向に並べたものは列ベクトルと呼びます。 一方、

\[{\bf z}=\begin{bmatrix} z_{1} & z_{2} & z_{3} \end{bmatrix}\]

のように、要素を横方向に並べたものは行ベクトルと呼びます。 本資料では、特に明示しない限り、単にベクトルと表現した場合には列ベクトルを指すものとします。 ベクトルに含まれるスカラの数のことを、そのベクトルの次元と呼びます。 例えば、\({\bf x}\)は3次元の列ベクトル、\({\bf z}\) は3次元の行ベクトルです。 スカラの場合と同様に、ベクトル \({\bf x}\) が\(N\)次元のベクトルで、ベクトルを構成するスカラが実数であることを、数式を用いて「\({\bf x}\in \mathbb{R}^N\)」とも書きます。

行列 (matrix) は同じサイズのベクトルを複数個並べたものです。例えば、

\[\begin{split}{\bf X} = \begin{bmatrix} x_{11} & x_{12} \\ x_{21} & x_{22} \\ x_{31} & x_{32} \end{bmatrix}\end{split}\]

は行列の一例です。行列は大文字、または大文字の太文字で表記することでスカラやベクトルと区別します。 行列の形（サイズ）は行数と列数で表現します。 例えば、上に挙げた \({\bf X}\) は行ベクトルが 3 つ並んだものと見ることができます。 そのため、 \({\bf X}\) の行数は 3 です。 一方、見方を変えると \({\bf X}\) は列ベクトルが 2 つ並んだものと見ることもできますので、 \({\bf X}\) の列数は 2 です。 そこで、 \({\bf X}\) を「 3 行 2 列の行列」と呼びます。 「サイズが \((3, 2)\) である行列」や「サイズが \(3\times 2\) の行列」と呼んでも構いません。 \(N\) 次元の列ベクトルはサイズが \((N, 1)\) の行列、 \(N\) 次元の行ベクトルはサイズが \((1, N)\) の行列と見ることができます。 スカラ、ベクトルの場合と並行して、行列 \({\bf X}\) のサイズが \((N, M)\) であり、各要素が実数であることを、「\({\bf X} \in \mathbb{R}^{N \times M}\)」 とも書きます。例えば、先程の \({\bf X}\) については \({\bf X}\in \mathbb{R}^{3\times 2}\) です。

テンソル (tensor) はベクトルや行列を一般化した概念です。 例えば、ベクトルは 1 方向に、行列は 2 方向にスカラが並んでいます。これは「ベクトルは 1 階のテンソルで、行列は 2 階のテンソルである」であることを意味します。 この考え方をさらに進めて、下図のように行列を奥行き方向にさらに並べたものを3階のテンソルと呼びます。例えば、カラー画像をデジタル表現する場合、1 枚の画像は RGB (Red Green Blue) の3枚のレイヤー（チャンネルと呼びます）を持つのが一般的です。 各チャンネルは行列として表され、その行列がチャンネル方向に複数積み重なっているため、画像は 3 階テンソルとみなすことができます。 3 階のテンソルは、特定の要素を指定するのに「上から 3 番目、左から 2 番目、手前から 5 番目」のように整数（インデックス）を3個必要とします。

同様に、4 次元以上の場合でも、\(N\) 次元にスカラを並べたもの（つまり、要素を指定するのに \(N\) 個のインデックスが必要なもの）を \(N\) 階のテンソルと言います。例えば、多くのディープラーニングフレームワークでは、複数枚の画像の集まりを「画像のインデックス1つ」+「各画像のインデックス 3 つ（幅、高さ、チャンネル）」の 4 階テンソルとして表現します。 前述のようにベクトルや行列はテンソルの一種とみなすことができますが、本資料では単に「テンソル」と言った場合は3階以上のテンソルを指します。

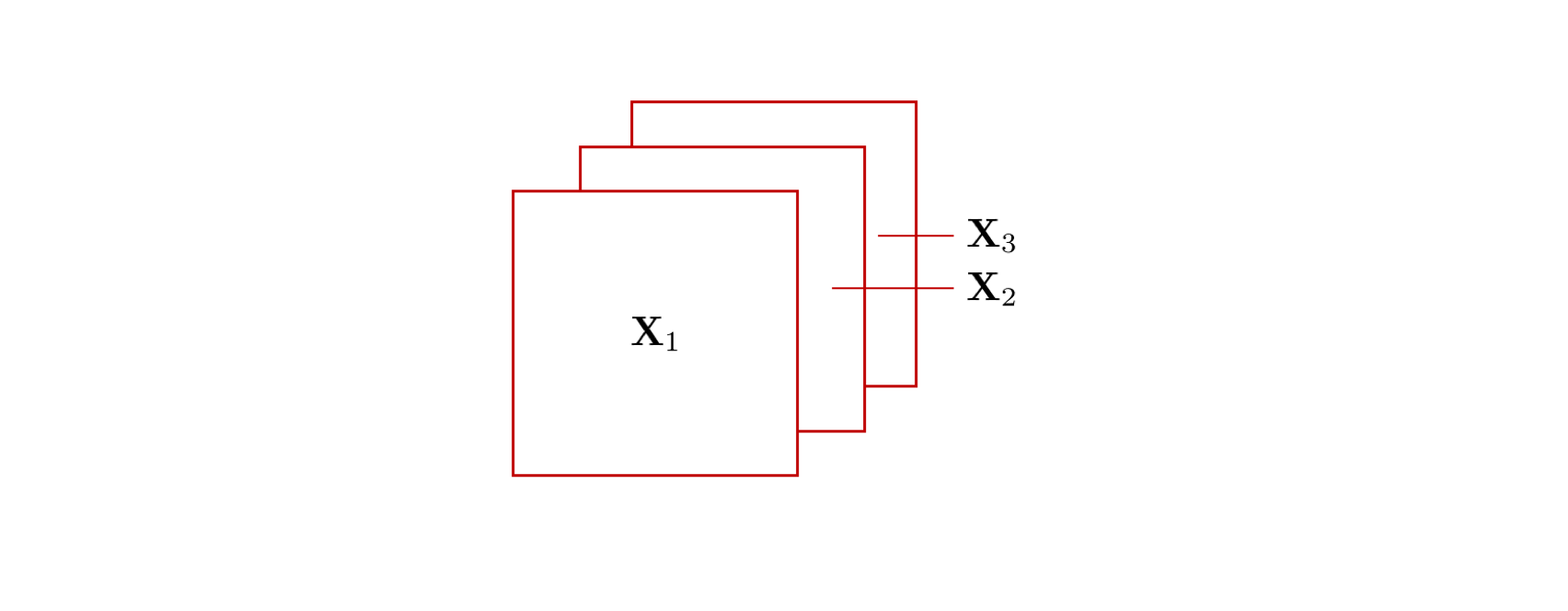
変数の形と字体の関係

多くの教科書（特に線形代数の教科書）では、変数を一目見てその型が何かがわかるように、特定の形（ベクトル、行列など）の変数には特定の字体を用いるという工夫がされています。 本資料に限らず、数式を追う時には変数の字体を見て、その変数の形を意識するのがおすすめです。 変数の形と字体の対応関係は教科書によって流派がありますが、以下にその一例を紹介します（本資料もこの規約に従います）。

字体	小文字	大文字
細字	スカラの変数 (\(a, b\) など)	スカラの定数 (\(A, B\) など)
太字	ベクトル (\({\bf x}, {\bf y}\) など)	行列、テンソル (\({\bf A}, {\bf B}\) など)

加算・減算・スカラ倍

次に、ベクトル、行列、テンソルの演算について解説します。 加算（足し算）及び減算（引き算）は同じサイズのベクトル同士、行列同士、テンソル同士の間だけで成立します。 以下に、行列およびベクトル同士の加算を具体例で示します。

ベクトル同士の加算

\[\begin{split}\begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix}+\begin{bmatrix} 4 \\ 5 \\ 6 \end{bmatrix}=\begin{bmatrix} 1 + 4 \\ 2 + 5 \\ 3 + 6 \end{bmatrix}=\begin{bmatrix} 5 \\ 7 \\ 9 \end{bmatrix}\end{split}\]

行列同士の加算

\[\begin{split}\begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix}+\begin{bmatrix} 7 & 8 & 9 \\ 10 & 11 & 12 \end{bmatrix}=\begin{bmatrix} 1+7 & 2+8 & 3+9 \\ 4+10 & 5+11 & 6+12 \end{bmatrix}=\begin{bmatrix} 8 & 10 & 12 \\ 14 & 16 & 18 \end{bmatrix}\end{split}\]

このように、加算、減算ではベクトル（行列/テンソル）の同じ位置にある要素同士に演算を行います。 このような計算は、要素ごとの (element-wise) 計算とも呼ばれています。 ベクトル（行列/テンソル）のサイズが異なる場合、計算が定義できないことに注意してください。

スカラ倍とはベクトル、行列、テンソルにスカラを掛ける演算です。 例えば、スカラ \(k\) に対し、「ベクトル \({\bf x}\) の \(k\) 倍」とは、ベクトルの各要素に\(k\)を掛ける操作です。 行列やテンソルの場合も同様に要素ごとに同じスカラ\(k\)を掛けます。 言葉で説明するよりも以下の具体例を見る方がわかりやすいかもしれません。

ベクトルのスカラ倍

\[\begin{split}10 \begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix}=\begin{bmatrix} 10 * 1 \\ 10 * 2 \\ 10 * 3 \end{bmatrix}=\begin{bmatrix} 10 \\ 20 \\ 30 \end{bmatrix}\end{split}\]

行列のスカラ倍

\[\begin{split}10 \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix}=\begin{bmatrix} 10 * 1 & 10 * 2 & 10 * 3 \\ 10 * 4 & 10 * 5 & 10 * 6 \end{bmatrix}=\begin{bmatrix} 10 & 20 & 30 \\ 40 & 50 & 60 \end{bmatrix}\end{split}\]

スカラ倍を行う前後でベクトル（行列/テンソル）のサイズは変化しないことに注意してください。

内積

同じサイズの2つのベクトルには、内積 (inner product) という演算が定義できます。 これは、それぞれのベクトルの同じ位置に対応する要素同士を掛け、それらを足し合わせる計算です。 \({\bf x}\) と \({\bf y}\) の内積は \({\bf x}\cdot {\bf y}\) で表されます。 例えば、以下の例では 3 次元のベクトルの内積を計算しています。

\[\begin{split}\begin{aligned}& \begin{bmatrix} 1 & 2 & 3 \end{bmatrix} \cdot \begin{bmatrix} 4 \\ 5 \\ 6 \end{bmatrix} = 1 \times 4 + 2 \times 5 + 3 \times 6 = 32 \end{aligned}\end{split}\]

2 つのベクトルの内積はスカラになることに注意してください。 上の例で示しているように、内積を考える時には 1 つ目のベクトルを行ベクトル（つまり、スカラを横に並べたベクトル）と思うと都合が良いです。これは次に説明する行列積に関連します。このように書いた場合には内積を表す \(\cdot\) は省略できます。

行列積

行列の乗算には、行列積、外積、要素積（アダマール積）など複数の方法があります。 ここではそのうち、線形代数や機械学習の多くの問題で登場します行列積について説明します。 以降では明示しない限り、「行列の掛け算」と言ったときには行列積を指すこととします。

行列 \({\bf A}\) と行列 \({\bf B}\) の行列積は \({\bf AB}\) と書き 、\({\bf A}\) の各行と \({\bf B}\) の各列の内積を並べたものとして定義されます。 例えば、行列 \({\bf A}\) の 1 行目の行ベクトルと、行列 \({\bf B}\) の 1 列目の列ベクトルの内積の結果は、\({\bf A}\) と \({\bf B}\) の行列積の結果を表す行列 \({\bf C}\) の 1 行 1 列目に対応します。

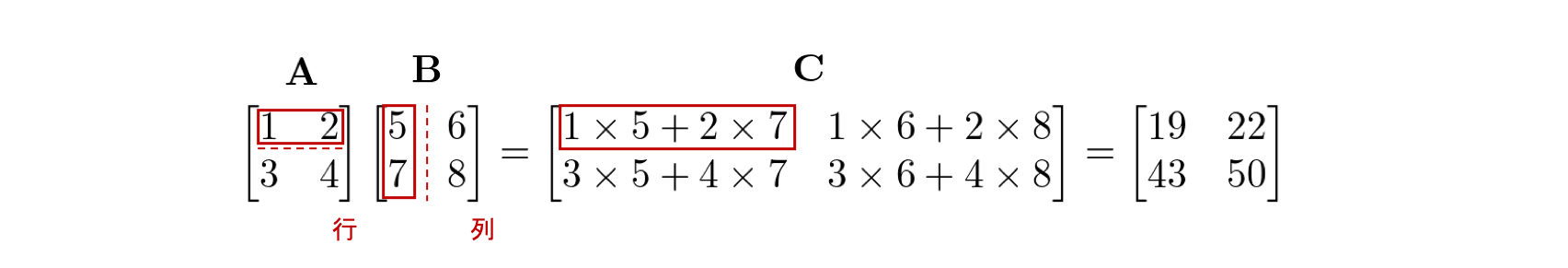
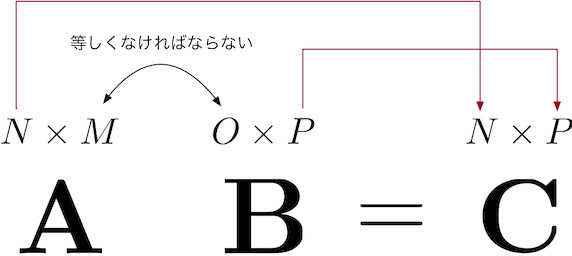
内積が定義される条件はベクトルのサイズが等しくなければなりませんでした。ここでもそれが成り立たなければなりません。具体的には、\({\bf A} \in \mathbb{R}^{N \times M}\), \({\bf B} \in \mathbb{R}^{O \times P}\) の時、\({\bf A} {\bf B}={\bf C}\) の行列積を定義するためには、\({\bf A}\) の列数 \(M\) と \({\bf B}\) の行数 \(O\) が一致する必要があります（注釈1）。 つまり、

\[M = O\]

でなければなりません。 そして、結果の行列 \({\bf C}\) の行数と列数は \({\bf A}\) の行数 \(N\) と \({\bf B}\) の列数 \(P\) とそれぞれ等しくなります。 すなわち、\({\bf C} \in \mathbb{R}^{N \times P}\) です。

2 つの \(N\) 次元ベクトル \({\bf x}, {\bf y}\) の内積は、 \({\bf x}\) をサイズ \((1, N)\) の行列（すなわち行ベクトル），\({\bf y}\) をサイズ \((N, 1)\) の行列（すなわち列ベクトル）とみなして行列積を行うことと考えることができます。 2 つのベクトルの行列積はサイズが \((1, 1)\) の行列、すなわちスカラとなります。これは 2 つのベクトルの内積の結果がスカラとなることと一致しています。

行列積は\({\bf AB}\) と \({\bf BA}\) が等しいとは限らないという点でスカラの掛け算と大きく異なります。例えば、

\[\begin{split}{\bf A} = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}, {\bf B} = \begin{bmatrix} 5 & 6 \\ 7 & 8 \end{bmatrix}\end{split}\]

とすると，

\[\begin{split}{\bf AB} = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \begin{bmatrix} 5 & 6 \\ 7 & 8 \end{bmatrix} = \begin{bmatrix} 1 * 5 + 2 * 7 & 1 * 6 + 2 * 8 \\ 3 * 5 + 4 * 7 & 3 * 6 + 4 * 8 \end{bmatrix} = \begin{bmatrix} 19 & 22 \\ 43 & 50 \end{bmatrix}\end{split}\]

\[\begin{split}{\bf BA} = \begin{bmatrix} 5 & 6 \\ 7 & 8 \end{bmatrix} \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} = \begin{bmatrix} 5 * 1 + 6 * 3 & 5 * 2 + 6 * 4 \\ 7 * 1 + 8 * 3 & 7 * 2 + 8 * 4 \end{bmatrix} = \begin{bmatrix} 23 & 34 \\ 31 & 46 \end{bmatrix}\end{split}\]

となり、 \({\bf AB} \not = {\bf BA}\) です。 掛け算の順序の違いを明示的に表現する場合、行列 \({\bf A}\) に行列 \({\bf B}\) を左から掛けること（ \({\bf BA}\) の計算）を行列 \({\bf B}\) を行列 \({\bf A}\) に左乗すると言い、右から掛ける場合は右乗すると言います。

\({\bf A}\) と \({\bf B}\) の選び方によっては \({\bf AB}\) と \({\bf BA}\) が等しくなる場合もあります。 例えば、

\[\begin{split}{\bf A} = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}, {\bf B} = \begin{bmatrix} 3 & 0 \\ 0 & 3 \end{bmatrix}\end{split}\]

とすると、

\[\begin{split}\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \begin{bmatrix} 3 & 0 \\ 0 & 3 \end{bmatrix} = \begin{bmatrix} 3 & 0 \\ 0 & 3 \end{bmatrix} \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} = \begin{bmatrix} 3 & 6 \\ 9 & 12 \end{bmatrix}\end{split}\]

となり、 \({\bf AB}\) と \({\bf BA}\) は一致します。ここで述べている注意は 「どんな \({\bf A}, {\bf B}\) でも\({\bf AB} = {\bf BA}\) が成立する」という主張は正しくないことを意味しています。

それでは、行列の計算条件も確認しながら、下記の 3 つの練習問題の計算を行ってください。

\[\begin{split}\begin{aligned} &\left( 1\right) \begin{bmatrix} 1 & 2 \end{bmatrix} \begin{bmatrix} 3 \\ 4 \end{bmatrix}\\ &\left( 2\right) \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}\begin{bmatrix} 5 \\ 6 \end{bmatrix}\\ &\left( 3\right) \begin{bmatrix} 1 & 2 \end{bmatrix}\begin{bmatrix} 3 & 4 \\ 5 & 6 \end{bmatrix}\begin{bmatrix} 3 \\ 1 \end{bmatrix} \end{aligned}\end{split}\]

こちらが解答です。

\[\begin{split}\begin{aligned} &\left( 1\right) \begin{bmatrix} 1 & 2 \end{bmatrix}\begin{bmatrix} 3 \\ 4 \end{bmatrix} = 1\times 3 + 2 \times 4 = 11\\ &\left( 2\right) \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}\begin{bmatrix} 5 \\ 6 \end{bmatrix} = \begin{bmatrix} 1 \times 5 + 2 \times 6 \\ 3 \times 5 + 4 \times 6 \end{bmatrix} = \begin{bmatrix} 17 \\ 39 \end{bmatrix}\\ &\left( 3\right) \begin{bmatrix} 1 & 2 \end{bmatrix}\begin{bmatrix} 3 & 4 \\ 5 & 6 \end{bmatrix}\begin{bmatrix} 3 \\ 1 \end{bmatrix} =\begin{bmatrix} 1 & 2 \end{bmatrix}\begin{bmatrix} 3 \times 3 + 4 \times 1 \\ 5 \times 3 + 6 \times 1 \end{bmatrix} = \begin{bmatrix} 1 & 2 \end{bmatrix}\begin{bmatrix} 13 \\ 21 \end{bmatrix} = 1 \times 13 + 2 \times 21 =55 \end{aligned}\end{split}\]

このような計算は、機械学習の基礎を学習していく過程でよく登場します。行列積では、演算前と後の行数・列数の変化に注意しましょう。

行列積によるベクトル・行列のサイズ変化

行列の前後では行列の形が変化します。 具体的にはサイズが \((L, M)\) と \((M, N)\) の行列の行列積の結果はサイズが \((L, N)\) の行列となります。 先ほどの 3 つの練習問題では、行列やベクトルの形・サイズがどのように変化していたかを確認してみましょう。

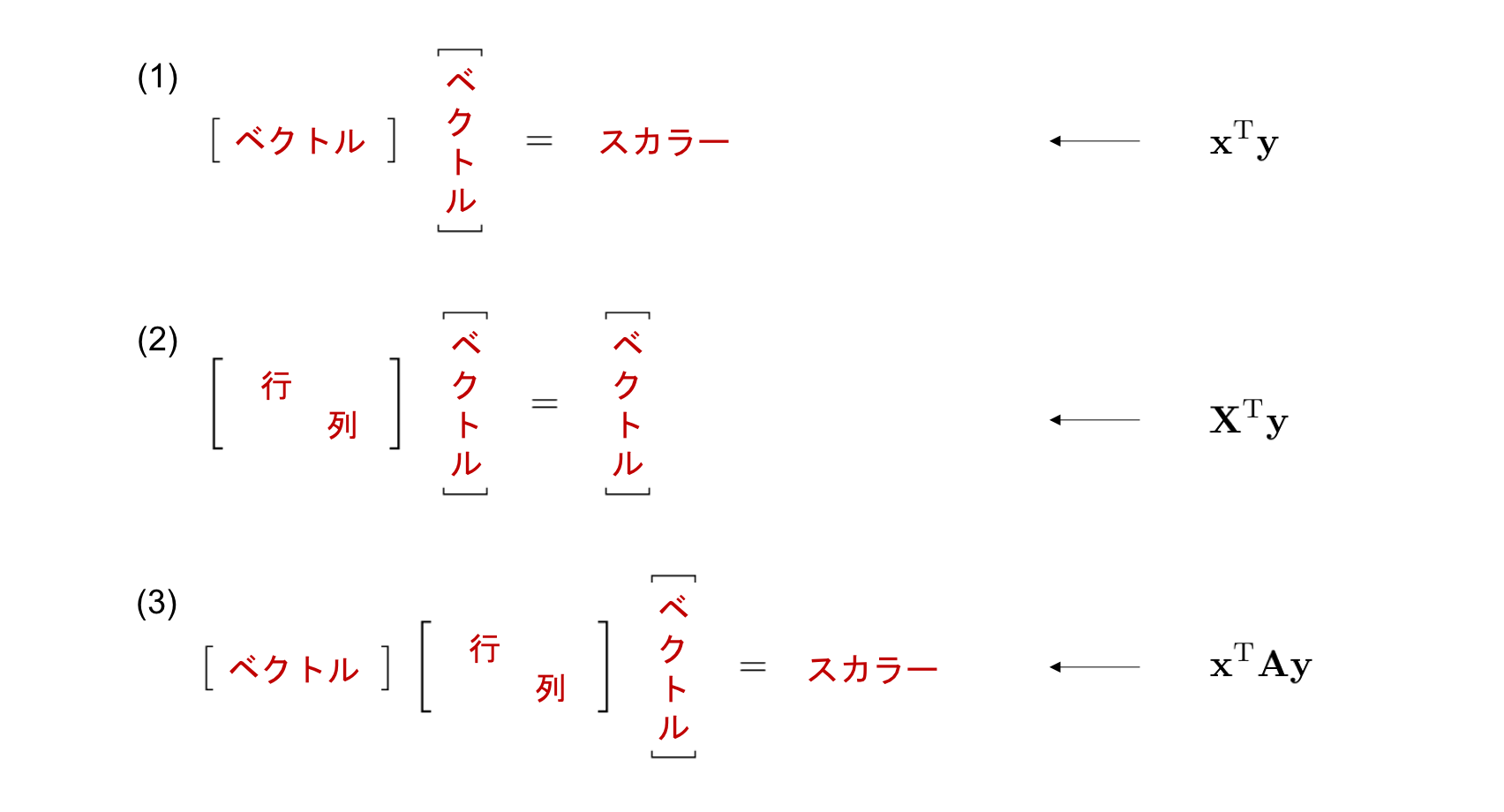
特に (3) では、一番左端のベクトルと、真ん中の行列の乗算結果が、行ベクトルであるため、サイズの変化が (1) と同じケースに帰着することに注意してください。

また、例えば \((3, 1)\) の行列のようにある次元のサイズが 1 となった場合、その次元を削除する場合があります。例えば (2)の計算結果はサイズが \((2, 1)\) の行列ですが、これは2次元のベクトルとして扱えます。同様に、 (1), (3) の答えはサイズ \((1, 1)\) の行列ですが、スカラとみなすことができます。このようにサイズが 1 になった次元をつぶす操作をしばしば squeeze と呼びます。

転置

ベクトルは縦方向に要素が並んだ列ベクトルを基本としていましたが、横方向に要素が並んだ行ベクトルを使いたい場合もあります。そこで列ベクトルを行ベクトルに、行ベクトルを列ベクトルに変換する操作を転置 (transpose) と呼びます。転置はベクトルの右肩に \({\rm T}\) と書くことで表します。例えば、 \({\bf x}\) が 3 次元のベクトルならば、

\[\begin{split}{\bf x} =\begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix}, \ {\bf x}^{\rm T} = \begin{bmatrix} 1 & 2 & 3 \end{bmatrix}\end{split}\]

です。 転置は行列に対しても定義できます。例えば、

\[\begin{split}{\bf X} =\begin{bmatrix} 1 & 4 \\ 2 & 5 \\ 3 & 6 \end{bmatrix}, \ {\bf X}^{\rm T}=\begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix}\end{split}\]

です。行列に対する転置では、行と列が入れ替わるため、サイズが \((N, M)\) だった行列は、転置するとサイズが \((M, N)\) の行列となります。つまり、 \(i\) 行 \(j\) 列目の値が転置後には \(j\) 行 \(i\) 列目の値になります。転置の公式として次を覚えておきましょう。

\[\begin{split}\begin{aligned} &\left( 1\right) \ \left( {\bf A}^{\rm T} \right)^{\rm T} = {\bf A} \\ &\left( 2\right) \ \left( {\bf A}{\bf B} \right)^{\rm T} = {\bf B}^{\rm T}{\bf A}^{\rm T}\\ &\left( 3\right) \ \left( {\bf A}{\bf B}{\bf C} \right)^{\rm T} = {\bf C}^{\rm T}{\bf B}^{\rm T}{\bf A}^{\rm T} \end{aligned}\end{split}\]

転置を用いると、 2 つの列ベクトル \({\bf x}\), \({\bf y}\) の内積 \({\bf x}\cdot {\bf y}\) は、行列積を用いて \({\bf x^{\rm T} y}\) と書けることに注意してください。

単位行列

スカラ値の \(1\) は、 \(10 \times 1 = 10\) のように、任意の数を \(1\) に乗じても値が変化しないという性質を持ちます。行列の演算において、これと同様の働きをする行列が単位行列 (identity matrix, unit matrix) です（注釈2）。 単位行列は

\[\begin{split}{\bf I} = \begin{bmatrix} 1 & 0 & \cdots & 0 \\ 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 1 \end{bmatrix}\end{split}\]

という形をしており、記号 \({\bf I}\) で表すのが一般的です。行列の斜めの要素を対角要素とよび、それ以外の要素を非対角要素とよびます。単位行列は、対角要素が全て \(1\) で、非対角要素が全て \(0\) であるような 正方行列（行数と列数が等しい行列）です。例えば、\(2 \times 2\) の単位行列は、

\[\begin{split}{\bf I} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}\end{split}\]

であり、\(3 \times 3\)の単位行列は、

\[\begin{split}{\bf I} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}\end{split}\]

です。行列のサイズを明示したい場合には、 \(I_n\) （ \(n \times n\) の単位行列の意味）と添字でサイズを表記することがあります。

単位行列はサイズが等しい任意の正方行列 \({\bf A}\) に対して以下の計算が成立します。

\[\begin{split}\begin{aligned} {\bf A}{\bf I} &= {\bf A} \\ {\bf I}{\bf A} &= {\bf A} \end{aligned}\end{split}\]

適当な行列で、単位行列を掛けても元の行列と値が変わらないことを確認してみましょう。

\[\begin{split}\begin{aligned} \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} &= \begin{bmatrix} 1 \times 1 + 2 \times 0 & 1 \times 0 + 2 \times 1 \\ 3 \times 1 + 4 \times 0 & 3 \times 0 + 4 \times 1 \end{bmatrix} \\ &= \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \end{aligned}\end{split}\]

計算結果から分かる通り、元の行列と全ての要素が一致しました。 \({\bf I}\) を左から掛けても同様の結果となることを確かめてみてください。

逆行列

\(0\) でないスカラ \(x\) には、 逆数 \(x^{-1}\) を考えることができます。 行列で逆数に対応するものが 逆行列 (inverse matrix) です。

厳密な定義は次の通りです。行列 \({\bf A}\) に対し、 \({\bf AB} = {\bf I}\) , \({\bf BA} = {\bf I}\) を満たす行列 \({\bf B}\) のことを \({\bf A}\) の逆行列 といいます。 このような条件を満たす行列 \({\bf B}\) は 行列 \({\bf A}\) によって存在したり存在しなかったりします。 しかし、もし \({\bf A}\) に対しこの条件を満たす行列が存在するならば、そのような行列はただ 1 つであることが知られています。 そこで、行列 \({\bf A}\) の逆行列を \({\bf A}^{-1}\) と書きます。

逆行列の定義から、

\[\begin{split}\begin{aligned} {\bf AA}^{-1} = {\bf I} \\ {\bf A}^{-1}{\bf A} = {\bf I} \end{aligned}\end{split}\]

が成立することに注意してください。ここで、 \({\bf I}\) は単位行列です。

逆行列が存在するような行列のことを正則行列と呼びます。 正則行列となるには少なくとも行列積 \({\bf AA^{-1}}\) と \({\bf A^{-1}A}\) の両方が定義されていなければなりません。 これは \({\bf A}\) は正方行列（つまり、行数と列数が同じ行列）であることを意味します （なぜか考えてみてください）。 しかし、 \({\bf A}\) の行数と列数が同じであるからと言って、常に \({\bf A}\) が正則行列とは限りません。 行列が正則であるための条件に関する詳細な説明はここでは省略します。

サイズが \(2 \times 2\) や \(3 \times 3\) といった小さな行列の場合には、手計算でも可能な逆行列計算の方法が知られていますが、機械学習ではより大きなサイズの行列（ \(1000 \times 1000\) など）を扱うことがあり、そういった大きな行列の逆行列を効率的または近似的にコンピュータを使って計算する手法が研究されています。

線形結合と二次形式

機械学習の数式で頻出する形式として、 \({\bf b}^{\rm T}{\bf x}\) と \({\bf x}^{\rm T}{\bf A}{\bf x}\) の 2 つがあります。 前者は線形結合もしくは一次結合、後者は二次形式と呼ばれています。 スカラの一次式 (\(ax + b\)) や二次式 (\(ax^2 + bx + c\)) をベクトルに拡張したものと捉えると良いでしょう。

線形結合の計算を要素ごとに見てみると、

\[\begin{split}\begin{aligned} {\bf b} &= \begin{bmatrix} 1 \\ 2 \end{bmatrix},\ {\bf x} = \begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix}\\ {\bf b}^{\rm T}{\bf x} &= \begin{bmatrix} 1 & 2 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = x_1 + 2x_2 \end{aligned}\end{split}\]

のように \({\bf x}\) の要素である \(x_1\) および \(x_2\) に関して一次式となっています。

また、二次形式も同様に要素ごとに確認してみると、

\[\begin{split}\begin{aligned} {\bf A} &= \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix},\ {\bf x} = \begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix}\\ {\bf x}^{\rm T}{\bf A}{\bf x} &= \begin{bmatrix} x_1 & x_2 \end{bmatrix} \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} \\ &= \begin{bmatrix} x_1 & x_2 \end{bmatrix} \begin{bmatrix} x_1 + 2x_2 \\ 3x_1 + 4x_2 \end{bmatrix} \\ &= x_1 \left( x_1 + 2x_2 \right) + x_2 \left( 3x_1 + 4x_2 \right) \\ &= x^2_1 + 5x_1 x_2 + 4x_2^2 \end{aligned}\end{split}\]

となり、各要素に関して二次式となっています。 一般に、\(x_1, \ldots, x_N\) に関する二次関数は、

\[\begin{split}{\bf x} = \begin{bmatrix} x_1 \\ \vdots \\ x_n \\ \end{bmatrix}\end{split}\]

として、

\[{\bf x}^{\rm T}{\bf A}{\bf x} + {\bf b}^{\rm T}{\bf x} + c\]

と表記できます。ここで、 \({\bf A}\) は 2次の項の係数を表すサイズ \((n, n)\) の 行列、 \({\bf b}\) は1次の項の係数を表す \(n\) 次元のベクトル、 \(c\) はスカラの定数項です。

ベクトルによる微分と勾配

微分は入力が変化した場合の関数値の変化量から求められました。 これは関数の入力がベクトルである場合も同様です。 ベクトルを入力にとる関数の微分を考えてみましょう。 入力ベクトルの要素毎に出力に対する偏微分を計算し、それらを並べてベクトルにしたものが勾配 (gradient) です。

まず勾配に関する計算の具体例を見てみましょう。

\[\begin{split}\begin{aligned} {\bf b} &=\begin{bmatrix} 3 \\ 4 \end{bmatrix}, \ {\bf x} = \begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix}\\ {\bf b}^{\rm T}{\bf x} &= \begin{bmatrix} 3 & 4 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = 3x_1 + 4x_2 \end{aligned}\end{split}\]

この \({\bf b}^{\rm T}{\bf x}\) をベクトル \({\bf x}\) で微分したものを、

\[\frac{\partial}{\partial {\bf x}} \left( {\bf b}^{\rm T}{\bf x} \right)\]

と表します。 「ベクトルで微分」とは、ベクトルのそれぞれの要素で対象を微分し、その結果を要素に対応する位置に並べてベクトルを作ることです。 前述の例では、以下のように計算を行います。

\[\begin{split}\begin{aligned} \frac{\partial}{\partial {\bf x}} \left( {\bf b}^{\rm T} {\bf x} \right) &= \frac{\partial}{\partial {\bf x}} \left( 3x_1 + 4x_2 \right) \\ &= \begin{bmatrix} \frac{\partial}{\partial x_1} \left( 3x_1 + 4x_2 \right) & \frac{\partial}{\partial x_2} \left( 3x_1 + 4x_2 \right) \end{bmatrix} \end{aligned}\end{split}\]

各要素の計算を進めると、以下のようになります。本チュートリアルでは、ベクトルは原則として列ベクトルを用いるルールを採用していますが、ここでは微分した結果を行ベクトルで表していることに注意してください。これは、後で登場するベクトル値関数（ベクトルを出力とする関数）の微分を考えた場合との整合性をとるためです。

\[\begin{split}\begin{aligned} \frac{\partial}{\partial x_1} \left( 3x_1 + 4x_2 \right) &= \frac{\partial}{\partial x_1} \left( 3x_1 \right) + \frac{\partial}{\partial x_1} \left( 4x_2 \right) \\ &= 3 \times \frac{\partial}{\partial x_1} \left( x_1 \right) + 4x_{2} \times \frac{\partial}{\partial x_1} (1) \\ &= 3 \times 1 + 4x_{2} \times 0 \\ &= 3 \end{aligned}\end{split}\]

\[\begin{split}\begin{aligned} \frac{\partial}{\partial x_2} \left( 3x_1 + 4x_2 \right) &= \frac{\partial}{\partial x_2} \left( 3x_1 \right) + \frac{\partial}{\partial x_2} \left( 4x_2 \right) \\ &= 3x_{1} \times \frac{\partial}{\partial x_2} (1) + 4 \times \frac{\partial}{\partial ax_2} (x_{2}) \\ &= 3x_{1} \times 0 + 4 \times 1 \\ &= 4 \end{aligned}\end{split}\]

従って、計算結果を整理すると、以下のようになります。

\[\begin{aligned} \frac{\partial}{\partial {\bf x}} \left( {\bf b}^{\rm T}{\bf x} \right) &= \begin{bmatrix} \frac{\partial}{\partial x_1} \left( 3x_1 + 4x_2 \right) & \frac{\partial}{\partial x_2} \left( 3x_1 + 4x_2\right) \end{bmatrix} = \begin{bmatrix} 3 & 4 \end{bmatrix} = {\bf b}^{\rm T} \end{aligned}\]

もう一つ別の例を考えてみましょう。今度は定数スカラーをベクトルで微分します。

\[\begin{split}\begin{aligned} c &= 3 , {\bf x} = \begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix} \\ \frac{\partial}{\partial {\bf x}} \left( c \right) &= \begin{bmatrix} \frac{\partial}{\partial x_1} \left( 3 \right) & \frac{\partial}{\partial x_2} \left( 3 \right) \end{bmatrix} = \begin{bmatrix} 0 & 0 \end{bmatrix} = {\bf 0} \end{aligned}\end{split}\]

偏微分を行う対象に変数が含まれていない場合、その偏微分は \(0\) となります。要素が \(0\) のみで構成されたベクトルをゼロベクトルと言い、数字の \(0\) を太字にした \({\bf 0}\) で表します。

これらを踏まえて、機械学習で頻出する計算結果をまとめて覚えておきましょう。

\[\begin{split}\begin{aligned} &\left( 1 \right) \ \frac{\partial}{\partial {\bf x}} \left( c \right) = {\bf 0} \\ &\left( 2 \right) \ \frac{\partial}{\partial {\bf x}} \left( {\bf b}^{\rm T}{\bf x} \right) = {\bf b}^{\rm T} \\ &\left( 3 \right) \ \frac{\partial}{\partial {\bf x}} \left( {\bf x}^{\rm T}{\bf A}{\bf x} \right) = {\bf x}^{\rm T} \left( {\bf A} + {\bf A}^{\rm T} \right) \end{aligned}\end{split}\]

ここで、(1) と (2) はすでに導出済みです。(3) は導出が少し複雑なので省略しますが、数値を代入して確認してみてください。

ベクトルを入力とする関数

前節で考えた \({\bf b^T x}\) や \({\bf x^T A x}\) は ベクトル \({\bf x}\) を受け取って、スカラ \({\bf b^T x}\), \({\bf x^T A x}\) を出力する関数と考えることができます。 \({\bf x}\) を成分表示して

\[\begin{split}{\bf x} = \begin{bmatrix} x_1 \\ x_2 \end{bmatrix}\end{split}\]

と書くと、この関数は 2 つのスカラ変数 \(x_1\), \(x_2\) を入力とする多変数関数です。 同様に、入力が \(M\) 個のスカラ変数の関数は、 \(M\) 次元のベクトル 1 個を入力とする関数とも解釈することができます。 多変数関数 \(f(x_1, \ldots, x_M)\) は、入力をまとめて

\[\begin{split}{\bf x} = \begin{bmatrix} x_1 \\ \vdots \\ x_M \end{bmatrix}\end{split}\]

と書き、 \(f({\bf x})\) と表記しても構いません。 \(f({\bf x})\) の微分は、前章で説明した偏微分を各変数 \(x_1, \ldots, x_M\) に対して行い

\[\begin{split}\frac{\partial}{\partial {\bf x}} f({\bf x}) = \begin{bmatrix} \frac{\partial}{\partial x_1} f({\bf x}) & \dots & \frac{\partial}{\partial x_M} f({\bf x}) \\ \end{bmatrix}\end{split}\]

と計算します。

ベクトル値関数

次に入力ではなく出力が多変数の関数を考えます。 まず、1 つのスカラ変数 \(x\) を入力とし、 \(N\) 個のスカラ（つまり、 \(N\) 次元のベクトルを 1 個）を出力する関数 \({\bf f}(x)\) を考えます。 ベクトル変数は \({\bf y}\) などの太字で書いていました。それと同様に、この関数も出力がベクトルであることを強調して \({\bf f}\) と太字で表します。 \({\bf f}\) のように出力がベクトルである関数を ベクトル値関数 (vector-valued function) と呼びます。それに対し、出力がスカラである関数を（そのことを強調したい場合には） スカラ値関数 (scalar-valued function) と呼びます。

\({\bf f}\) の出力の各成分に注目すると、 \({\bf f}\) は \(N\) 個のスカラ値関数の集まりと考えることができます。 つまり、 \(x\) を受け取り、 \({\bf f}\) の 第 \(n\) 成分を出力する関数を \(f_n\) と書くと、

\[\begin{split}{\bf f}(x) = \begin{bmatrix}f_1(x) \\ \vdots \\ f_N(x)\end{bmatrix}\end{split}\]

です。 入力が多変数でも同様に成分表示することができます。すなわち、入力変数が \(M\) 次元ベクトル、出力変数が \(N\) 次元ベクトルである関数 \({\bf g}\) は

\[\begin{split}{\bf g}({\bf x}) = \begin{bmatrix}g_1({\bf x}) \\ \vdots \\ g_N({\bf x})\end{bmatrix} = \begin{bmatrix}g_1(x_1, \ldots, x_M) \\ \vdots \\ g_N(x_1, \ldots, x_M)\end{bmatrix}\end{split}\]

と成分表示できます。誤解が生じないならば、一番右の表式のように入力変数 \({\bf x}\) を成分表示しても構いません。

ベクトル値関数の微分

ベクトル値関数の微分を行うには、各成分ごとにスカラ値関数と同様の方法で微分します。例えば前節の \({\bf f}\) の微分は

\[\begin{split}{\bf f}'(x) = \begin{bmatrix} f'_1(x) \\ \vdots \\ f'_N(x) \end{bmatrix}\end{split}\]

です。出力がベクトルであることに対応して、微分もベクトルであることに注意してください。 微小量を表す \(d\) を用いて

\[\begin{split}\frac{d}{dx} {\bf f} (x) = \begin{bmatrix} \frac{d}{dx}f_1(x) \\ \vdots \\ \frac{d}{dx}f_N(x) \end{bmatrix}\end{split}\]

と書いても構いません。

入出力が共に多変数である関数を微分する場合も、出力の成分ごとに微分します。 ただし、今度は入力も多変数であるため、入力の成分ごとに偏微分を行わなければなりません。 例えば、前節の \({\bf g}\) を微分すると、前節の成分表示を用いて

\[\begin{split}\frac{\partial {\bf g}}{\partial {\bf x}}({\bf x}) = \begin{bmatrix} \frac{\partial g_{1}}{\partial {x_1}}({\bf x}) & \cdots & \frac{\partial g_{1}}{\partial {x_M}}({\bf x}) \\ \vdots & \ddots & \vdots \\ \frac{\partial g_{N}}{\partial {x_1}}({\bf x}) & \cdots & \frac{\partial g_{N}}{\partial {x_M}}({\bf x}) \end{bmatrix}\end{split}\]

となります。 \(M\) 個の入力変数と \(N\) 個の出力変数の組み合わせを考える必要があるので、微分はサイズ \((N, M)\) の行列となることに注意してください。この、すべての偏微分の組み合わせをまとめて作った行列のことを ヤコビ行列 と呼びます。

合成関数の微分（多変数バージョン）

先程 1 変数入力、1 変数出力の合成関数の微分（連鎖律）を説明しました。 類似の定理が多変数入力、多変数出力の場合にも成立します。 本節では多変数バージョンの合成関数の微分の公式を紹介します。

\({\bf g}\) を \(M\) 変数入力 \(N\) 変数出力、\({\bf f}\) を \(N\) 変数入力 \(L\) 変数出力の関数とします。 これらの関数の合成 \({\bf h} = {\bf f}({\bf g} ({\bf x}))\) は \(M\) 変数入力 \(L\) 変数出力の関数であることに注意してください。 これを \(x\) で微分します。 以下の式が多変数関数バージョンの合成関数の微分の公式です。

\[\frac{\partial {\bf h}}{\partial {\bf x}}({\bf x}) = \frac{\partial {\bf f}}{\partial {\bf u}}({\bf u}) \frac{\partial {\bf g}}{\partial {\bf x}}({\bf x}).\]

ここで、 \({\bf u} = {\bf g}({\bf x})\)です。

1 変数入力、1変数出力の場合の合成関数の微分の公式と見比べると細字だった変数や関数が太字となり \(d\) であった所が偏微分を表す \(\partial\) に置き換えられています。すなわち、 1 変数の場合との最も大きな違いは

\[\frac{\partial {\bf h}}{\partial {\bf x}}({\bf x}), \frac{\partial {\bf f}}{\partial {\bf u}}({\bf u}), \frac{\partial {\bf g}}{\partial {\bf x}}({\bf x})\]

が行列であることです。行列のサイズはそれぞれ \((L, M)\), \((L, N)\), \((N, M)\) です。 それに伴い、公式の右辺の掛け算は行列積です。サイズが \((L, N)\) と \((N, M)\) なので、行列積がきちんと定義できることに注意してください。 また、行列の積は交換可能ではないので、右辺を交換して \(\frac{\partial {\bf g}}{\partial {\bf x}}({\bf x}) \frac{\partial {\bf f}}{\partial {\bf u}}({\bf u})\) とすると別の意味になってしまう（そもそも定義することができないかもしれない）ことにも注意してください。

\(M = N = L = 1\) とすると、前節の合成関数の微分と全く同じ公式です。 その意味で多変数関数の合成関数の微分は 1 変数の場合を一般化した公式です。 逆に、1 変数の公式は多変数の公式の特別な場合と言うこともできます。

計算例1

合成関数の微分を使って、多変数関数の微分を具体的に計算してみましょう。

\[\begin{split}{\bf x} = \begin{bmatrix} x_1 \\ x_2 \end{bmatrix}, {\bf u} = \begin{bmatrix} u_1 \\ u_2 \\ u_3 \\ u_4 \end{bmatrix}\end{split}\]

として、

\[\begin{split}{\bf g}({\bf x}) = \begin{bmatrix} 3x_1 + 1 \\ 2x_2 + 4 \\ x_1 x_2 \\ 5 \end{bmatrix}, {\bf f}({\bf u}) = \begin{bmatrix} 2 u_1 + 1 \\ u_2^2 + u_3^2 \\ u_3 u_4 \end{bmatrix}\end{split}\]

とします。 つまり、\({\bf g}\) は 2 入力 4 出力、\({\bf f}\) は 4 入力 3 出力です。

これらについて \(\frac{\partial {\bf f}({\bf g}({\bf x}))}{\partial {\bf x}}\) を計算します。 偏微分を定義どおり計算すると

\[\begin{split}\begin{align*} \frac{\partial {\bf g}}{\partial {\bf x}} ({\bf x})&= \begin{bmatrix} \frac{\partial g_1}{\partial x_1} & \frac{\partial g_1}{\partial x_2} \\ \frac{\partial g_2}{\partial x_1} & \frac{\partial g_2}{\partial x_2} \\ \frac{\partial g_3}{\partial x_1} & \frac{\partial g_3}{\partial x_2} \\ \frac{\partial g_4}{\partial x_1} & \frac{\partial g_4}{\partial x_2} \end{bmatrix} = \begin{bmatrix} 3 & 0 \\ 0 & 2 \\ x_2 & x_1 \\ 0 & 0 \end{bmatrix}\\ \frac{\partial {\bf f}}{\partial {\bf u}} ({\bf u})&= \begin{bmatrix} \frac{\partial f_1}{\partial u_1} & \frac{\partial f_1}{\partial u_2} & \frac{\partial f_1}{\partial u_3} & \frac{\partial f_1}{\partial u_4}\\ \frac{\partial f_2}{\partial u_1} & \frac{\partial f_2}{\partial u_2} & \frac{\partial f_2}{\partial u_3} & \frac{\partial f_2}{\partial u_4}\\ \frac{\partial f_3}{\partial u_1} & \frac{\partial f_3}{\partial u_2} & \frac{\partial f_3}{\partial u_3} & \frac{\partial f_3}{\partial u_4}\\ \end{bmatrix} = \begin{bmatrix} 2 & 0 & 0 & 0\\ 0 & 2u_2 & 2u_3 & 0 \\ 0 & 0 & u_4 & u_3 \end{bmatrix} \end{align*}\end{split}\]

となります（行列中の \(\frac{\partial g_1}{\partial x_1}\) などは本来は \(\frac{\partial g_1}{\partial x_1}({\bf x})\) などと書くべきですが、式が煩雑になるため省略しました）。 よって、合成関数の微分の公式より、

\[\begin{split}\begin{align*} \frac{\partial {\bf f}({\bf g}({\bf x}))}{\partial {\bf x}} &= \begin{bmatrix} 2 & 0 & 0 & 0\\ 0 & 2u_2 & 2u_3 & 0 \\ 0 & 0 & u_4 & u_3 \end{bmatrix} \begin{bmatrix} 3 & 0 \\ 0 & 2 \\ x_2 & x_1 \\ 0 & 0 \end{bmatrix} \\ &= \begin{bmatrix} 6 & 0 \\ 2u_3x_2 & 4u_2 + 2u_3x_1 \\ u_4x_2 & u_4x_1 \end{bmatrix} \\ &= \begin{bmatrix} 6 & 0 \\ 2x_1x_2^2 & 2x_1^2x_2 + 8x_2 + 16 \\ 5x_2 & 5x_1 \end{bmatrix} \end{align*}\end{split}\]

となります。公式を適用する際に \({\bf u} = {\bf g}(\bf x)\) 、すなわち

\[\begin{split}\begin{bmatrix} u_1 \\ u_2 \\ u_3 \\ u_4 \end{bmatrix} = \begin{bmatrix} 3x_1 + 1 \\ 2x_2 + 4 \\ x_1 x_2 \\ 5 \end{bmatrix}\end{split}\]

を用いました。

計算例2

もう1つの例として、合成した関数の入出力が 1 変数となる場合、つまり、\(M = 1, L = 1\) の場合を考えてみましょう。 式を簡単にするために、 \(N = 2\) とします。 1 変数であることを強調して、 \({\bf u} = {\bf g}(x)\), \(y = f({\bf u})\) とスカラーとなる変数には小文字を用いることにします。 \(f\) と \({\bf g}\) を合成した関数を \(h(x) = f({\bf g}(x))\) とします。 \(h\) は 入出力が共に 1 変数なので、その微分を簡便に \(h'(x)\) と書くことにすると、合成関数の微分の公式は

\[\begin{split}\begin{align*} h'(x) &= \frac{\partial f}{\partial {\bf u}} ({\bf u}) \frac{d {\bf g}}{d x} (x)\\ &= \begin{bmatrix} \frac{\partial f}{\partial u_1} ({\bf u}) & \frac{\partial f}{\partial u_2} ({\bf u}) \end{bmatrix} \begin{bmatrix} \frac{d g_1}{d x} (x) \\ \frac{d g_2}{d x} (x) \end{bmatrix} \\ &= \frac{\partial f}{\partial u_1} ({\bf u})\frac{d g_1}{d x}(x) + \frac{\partial f}{\partial u_2} ({\bf u})\frac{d g_2}{d x}(x) \end{align*}\end{split}\]

と書き下すことができます（微分する変数が 1 つしかない場合は偏微分記号 \(\partial\) ではなく 1 変数微分 \(d\) を用いて書きました）。

本資料で紹介した合成関数の微分の公式の他にも行列やベクトルの計算で用いられる公式はたくさんあります。 それらの公式は The Matrix Cookbook などにまとまっていますので、論文等を読む際などにも必要に応じてこれらを参照すると良いでしょう。 また、ヤコビ行列の計算方法は The Matrix Calculus You Need For Deep Learningなどにまとまっています。

---

注釈 1

\(N \times M\) 行列、などと言われたときに、\(N\) と \(M\) のどちらが行で、どちらが列だろう？と迷ったときは、「行列」という言葉を再度思い浮かべて、「行→列」つまり先にくる \(N\) が行数で、\(M\) が列数だ、と思い出すのがおすすめです。

▲上へ戻る

注釈 2

文献によっては単位行列ではなく、すべての成分が1の行列のことをunit matrixと呼ぶこともあります。

▲上へ戻る