微分の基礎

微分と関数最小化の関係

前章で微分が目的関数の最小化に役立つと紹介しました。本節ではまず具体例を用いてそのことを直感的に理解しましょう。 例として、下図のような下向きにくぼんだ形をした関数がどこで最小値をとるかを探す問題を考えます。

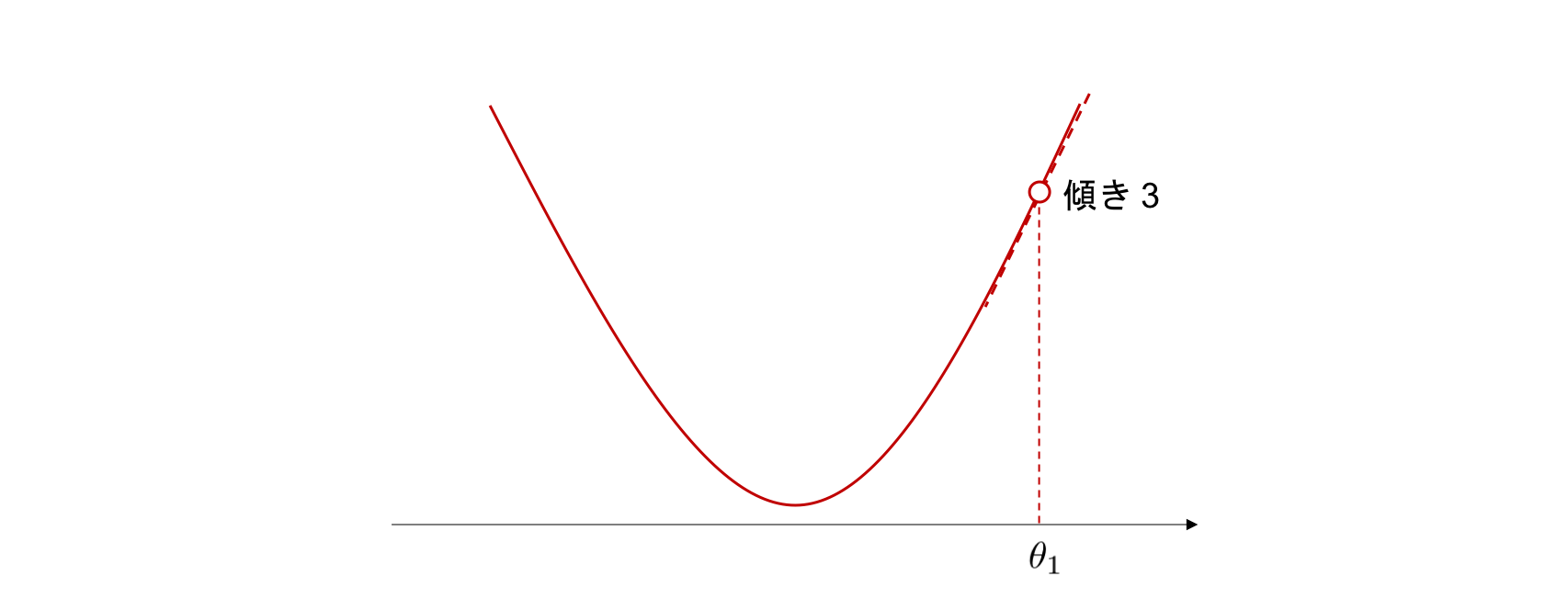
適当な点 \(\theta_{1}\) でこの関数のグラフに接する直線（接線）を考えます（注釈1）。 仮にこの接線の傾きが \(+3\) 、すなわち正の値であったとしましょう。この時、接線は右に進むほど高さが上がり，逆に左に進むほど高さが下がります。 \(\theta_{1}\) の周辺では、関数のグラフと接線は非常に近く、両者はほとんど見分けることができません。 すると、関数も接線と同じように \(\theta_{1}\) 右に進むと増加し，左に進むと減少していることがわかります。

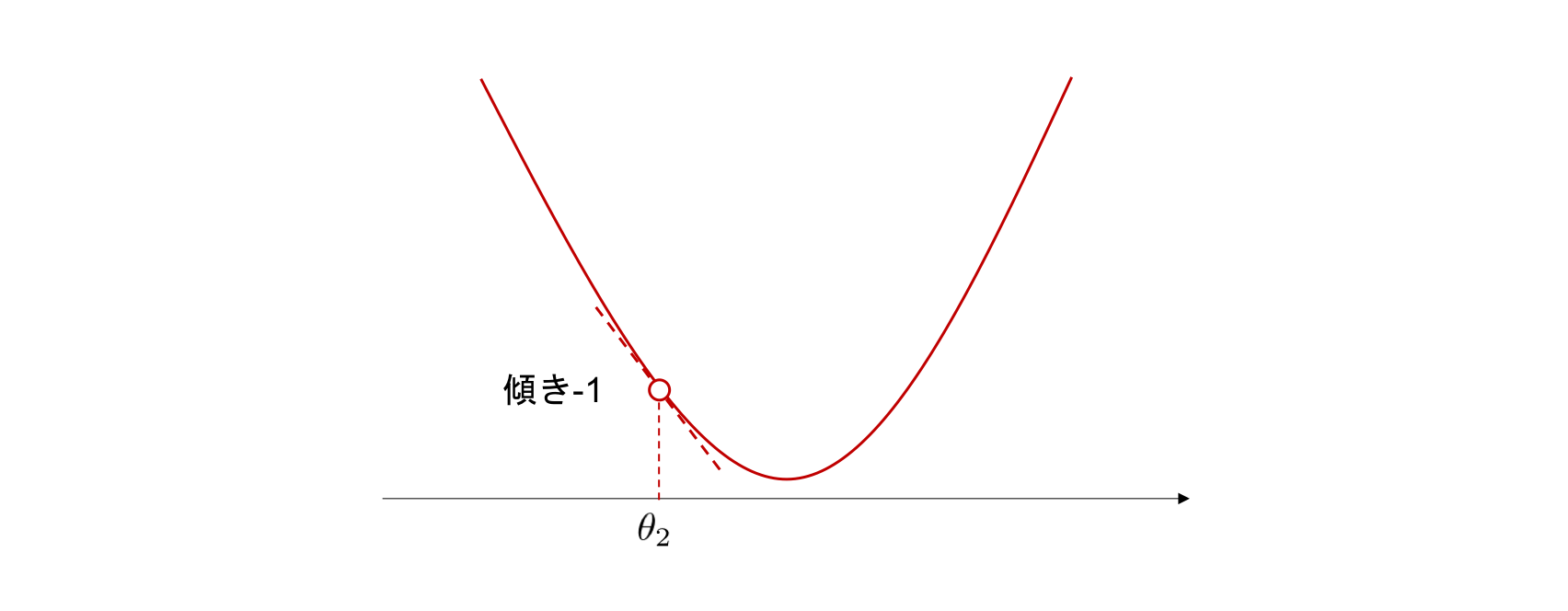
次に、グラフ上の別の点 \(\theta_{2}\) においてこのグラフに接する接線を考えます。 今度は接線の傾きが \(-1\) であるとします。傾きが負のため、接線は右肩下がりの直線です。 グラフは接線と非常に近いため、グラフも \(\theta_{2}\) の周辺では、同じように右肩下がりであるとわかります。

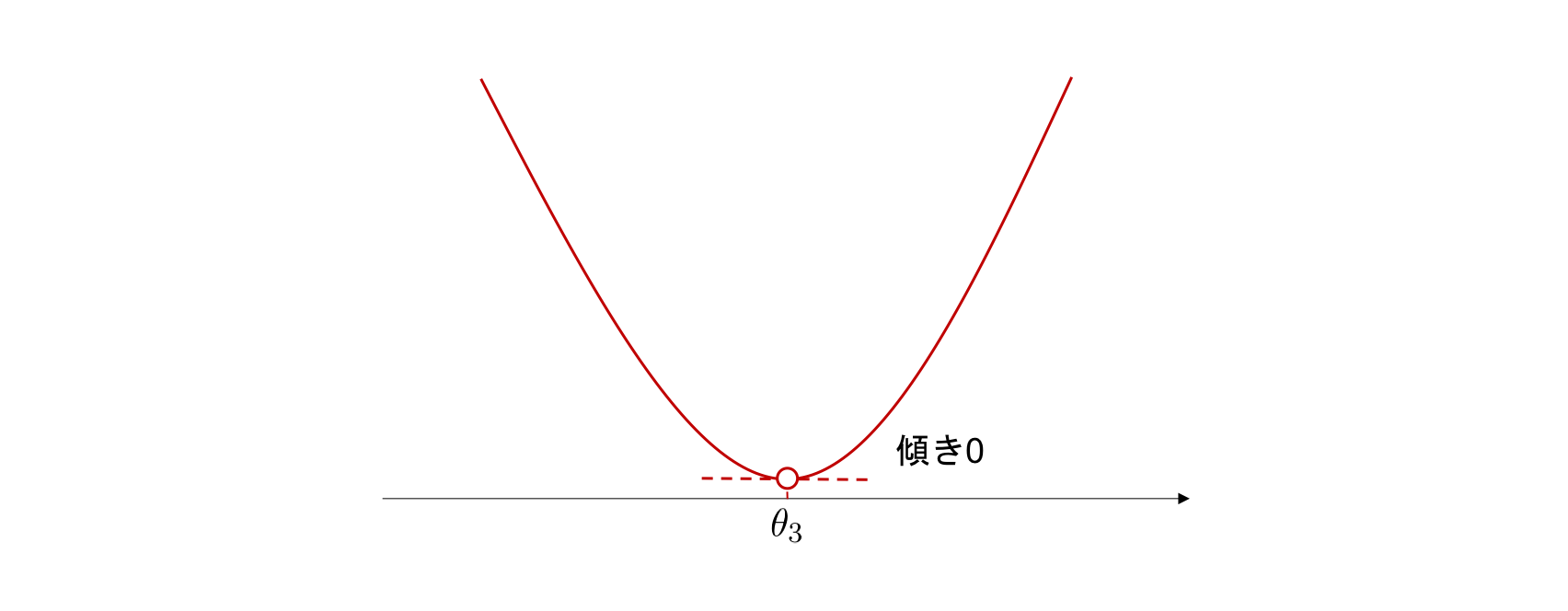
最後にちょうどグラフの谷となっている点 \(\theta_{3}\) を考えます。 図を見て分かる通り、関数はこの点で最小値を取ります。 一方、点 \(\theta_{3}\) でグラフに接する接線は水平、すなわち傾きが0です。

これまでの観察をまとめると、接線の傾きと関数の振る舞いには次の関係があることがわかります。

• ある点で接する接線の傾きが正ならば、その点の近くでグラフは右肩上がり（= 左に進むと高さが下がる）

• ある点で接する接線の傾きが負ならば、その点の近くでグラフは右肩下がり（= 右に進むと高さが下がる）

• 関数が最小値をとる点に接する接線の傾きは \(0\) である

つまり、関数の最小値をとる点を求める問題では、接線の傾きが \(0\) となる点が答えの候補（注釈2）となることがわかります。 本章で説明するように、微分を用いると接線の傾きを計算することができます。 このことから、微分が関数の最小化問題に有用なツールであることがわかります。

以降では、微分の定義と微分に関する公式を紹介します。さらに、入力が多変数の関数での微分（偏微分）についても解説します。

2 点間を通る直線の傾き

接線の傾きと微分の関係を調べるため、まずは2点を通る直線の傾きを求める問題を考えます。

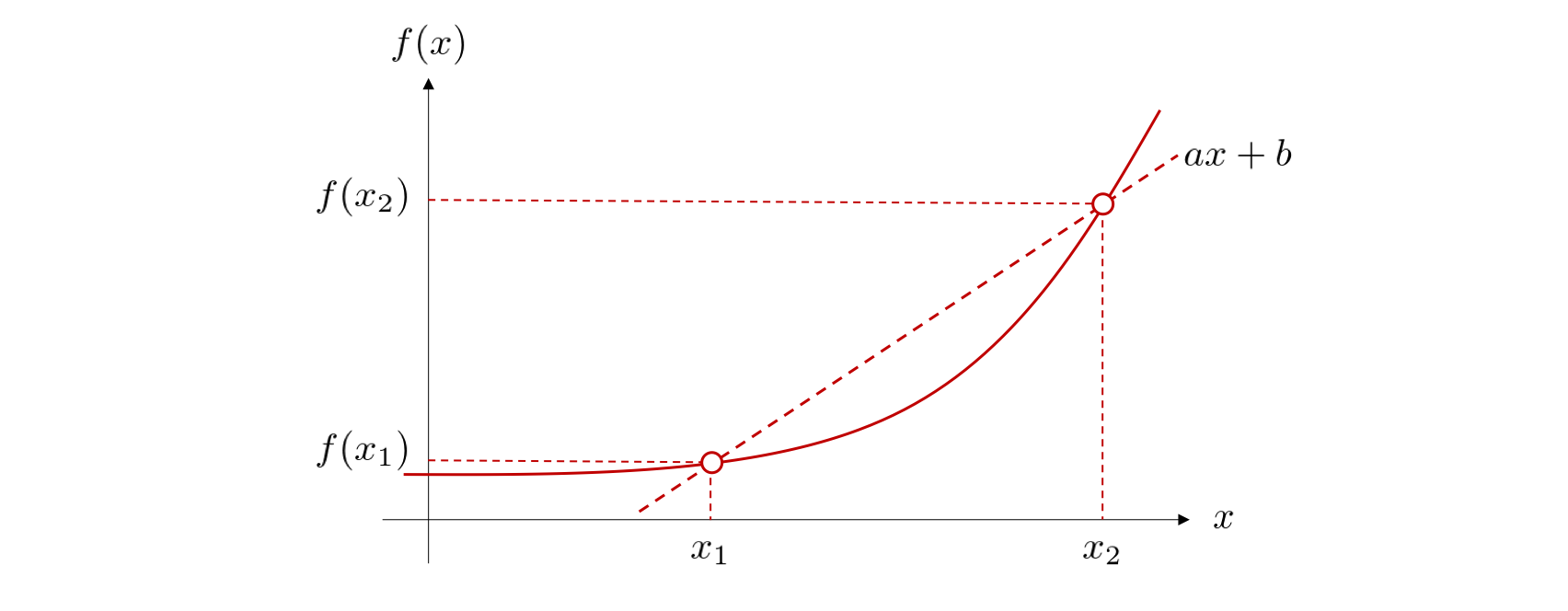
直線の傾きは 「\(y\) （縦方向）の増加量 / \(x\) （横方向）の増加量」で計算できるので、上図の直線の傾き \(a\) は、

\[a = \dfrac{f(x_{2}) - f(x_{1})}{x_{2}-x_{1}}\]

で求められます。

接線の傾き

上図での点 \(x_1\) における接線の傾きを求めるために、もう一方の点 \(x_2\) を \(x_1\) に近づけていきます。ただし、 \(x_1\) と \(x_2\) が完全に同じになってしまうと、\(x\) 方向、 \(y\) 方向の増加量がどちらも \(0\) になってしまうため、傾きは \(0/0\) で計算することができません。 そこで 2 点は異なる点でありつつ、 \(x_2\) を限りなく \(x_1\) に近づけていった時、直線の傾きがどのように振る舞うかを見る必要があります。これを数式的に表現するには、極限の考えが必要になります。

極限では、変数がある値に限りなく近づくとき、その変数によって記述される関数がどのような値に近づくかを考えます。 関数 \(f\) に対し、\(h\) という変数を \(a\) に近づけていったときの \(f(h)\) が近づく値を \(\lim\) という記号を用いて

\[\displaystyle \lim _{h\rightarrow a} f(h)\]

と書きます。例えば、 \(h\) を限りなく \(0\) に近づけた時に、 \(3h\) も限りなく \(0\) に近づいていきます。 従って

\[\displaystyle \lim _{h\rightarrow 0} 3h=0\]

です。もっと一般に \(n\) を自然数、 \(c\) を定数として、

\[\displaystyle \lim _{h\rightarrow a} c h^n=c a^n\]

が成立します。これだけ見ると単に関数 \(\lim _{h\rightarrow a} f(h)\) は \(h\) に \(a\) を代入した値 \(f(a)\) のように思えるかも知れません。しかし、今考えている直線の傾きの場合、そのような代入操作を行うと先程のように \(0/0\) の形が現れてしまうため、単純な代入では極限を求めることはできません。 極限の計算方法は後ほど詳しく解説します。

それでは、下図のある点 \(x\) における接線の傾き \(a\) を求めていきましょう。

2点を通る直線の傾きの式と極限を組み合わせて、接線の傾きを求めることができます。

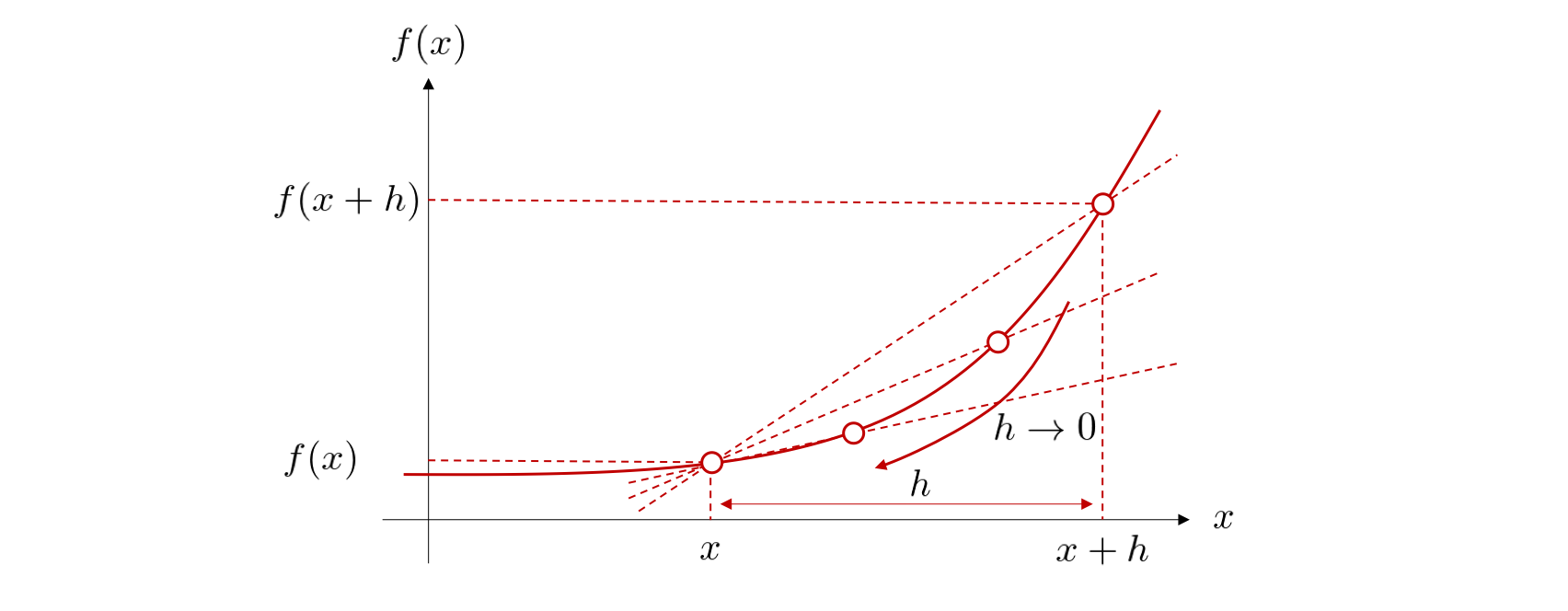
はじめに、 \(x\) から \(h\) だけ離れた点 \(x + h\) を考え、2点を通る直線の傾きを求めてみます。 次に \(h\) を \(0\) に限りなく近づけていけば、1点 \(x\) で接する接線を考えることができます。 これを式でみると

\[\begin{split}\begin{aligned} a &= \lim_{h \rightarrow 0} \frac{f(x + h) - f(x)}{(x + h) - x} \\ &= \lim_{h \rightarrow 0} \frac{f(x + h) - f(x)}{h} \\ \end{aligned}\end{split}\]

となります。よく見るとこの式は \(x\) を決めるごとにある1つの値を定めています、すなわちこの式は \(x\) の関数です（\(h\) は \(h\to 0\) の極限を取っているので \(h\) の関数にはなっていないことに注意してください）。 この式を \(f\) の 導関数 (derivative)と呼び、 \(f'(x)\) と書きます。すなわち、

\[f'(x)= \lim_{h \rightarrow 0} \frac{f(x + h) - f(x)}{h}\]

です。導関数を求めることを微分(differentiation)するといいます。 記号の使い方として、 \(f'(x)\) を

\[ \begin{align}\begin{aligned} \frac{d}{dx}f (x)\\または\end{aligned}\end{align} \]

\[\frac{df}{dx} (x)\]

と書いても構いません。 この \(d\) という記号は増分をとる操作を表しており、例えば \(dx\) は \(x\) の変化量を表します。 この記法は煩雑ですが、\(x, y\) など変数が複数ある場合、 どの変数で微分しているかが明確になるため、表現を正確にすることができます。

微分の公式

ある関数の導関数を計算するには、導関数の定義通りに計算するのが最も愚直な方法です． しかし、これから紹介する種々の公式を組み合わせることで、わざわざ定義に戻らなくても、複雑な関数の導関数を計算できます。 以下では、 \(c\) は定数、 \(x\) は変数を表します。

まずはじめに、以下の 3 つの公式を紹介します。

\[\begin{split}\begin{align} \left( c\right)^{'} &= 0 \\ \left( x\right)^{'} &= 1\\ \left( x^{2}\right)^{'} &= 2x \end{align}\end{split}\]

1つ目の左辺は定数関数 \(f(x) = c\) を \(x\) で微分した導関数を表しています。 定数関数のグラフを書くと \(x\) 軸に平行になるため、どの点で接線を引いてもその傾きは \(0\)です（グラフと接線は同一の直線となります）。これは導関数は 0 であることを意味します。これが 1 つ目の式の図形的な理解です。 同様に2つ目の公式は 「\(y=x\) のグラフではどの点で接線を引いても傾きが1」であることを意味します（この場合もグラフと接線は同一の直線です）。 極限の扱いに慣れるために、3番目の公式を証明しましょう。導関数の定義から左辺は

\[ \begin{align}\begin{aligned} \displaystyle \lim _{h\to 0} \frac{(x+h)^2 - x^2}{(x+h) - x}\\です。これは\end{aligned}\end{align} \]

\[\begin{align} \lim _{h\to 0} \frac{(x+h)^2 - x^2}{(x+h) - x} = \lim _{h\to 0} \frac{2xh + h^2}{h} = \lim _{h\to 0} (2x + h) \end{align}\]

と計算できます。ここで \(h\to 0\) 、すなわち \(h\) を限りなく \(0\) に近づけると、 \(2x + h\) は \(2x\) に限りなく近づいていきます。従って、 \(\left( x^{2}\right)^{'} = 2x\) が導かれました。

以下の公式も頻繁に利用します。

\[\begin{split}\begin{align} \left( x^{n} \right)^{'} &= nx^{n-1} \\ \left( e^{ax} \right)^{'} &= ae^{ax} \end{align}\end{split}\]

ここで、\(a\) は定数、 \(e\) は自然対数の底、もしくは ネイピア数 と呼ばれる特別な定数で、およそ \(2.71828\cdots\) です。 \(1\) つ目の公式で \(n=1, 2\)とすると、本節の最初に紹介した \(x\), \(x^2\) の微分の公式に帰着されることに注意してください。 \(e^{ax}\) は \(\exp(ax)\) のように表記されることがよくあります。その表記を用いると最後の公式は

\[\bigl( \exp(ax) \bigr)^{'} = a\exp(ax)\]

とも書けます。

線形性

微分は線形性という性質を持っています。 それがどのような性質なのか、具体例を挙げて見ていきましょう。 微分には線形性という性質によって、

\[(3x)' = 3 \times (x)'\]

のように定数項を微分の演算の外側に出すことができます。 また、

\[\left( 3x^{2} + 4x - 5 \right)' = \left( 3x^{2} \right)' + \left( 4x \right)' - \left( 5 \right)'\]

のように、加算や減算はそれぞれ項ごとに独立に微分の演算を行うことができます。 この 2 つの特性を合わせて線形性と呼びます。

もう少し微分の計算を練習してみましょう。

\[\begin{split}\begin{aligned} \left( 3x^{2} + 4x + 5 \right)' &= \left( 3x^{2} \right)' + \left( 4x \right)' - \left( 5 \right)' \\ &= 3 \times \left( x^{2} \right)' + 4 \times \left( x \right)' - 5 \times \left( 1 \right)' \\ &= 3 \times 2x + 4 \times 1 - 5 \times 0 \\ &= 6x + 4 \end{aligned}\end{split}\]

この線形性に関しては、下記のように公式としてまとめることができます。

\[\begin{split}\begin{align} \left( cf(x) \right)^{'} &= c f'(x) \\ \left( f(x) + g(x) \right)^{'} &= f^{'}(x) + g^{'}(x) \\ \end{align}\end{split}\]

2 つの関数の積の形で書かれている関数に関しては次の公式が成り立ちます。

\[\bigl( f(x) g(x) \bigr)^{'} = f^{'}(x)g(x) + f(x)g^{'}(x)\]

関数 \(f\) の導関数と関数 \(g\) の導関数がわかれば、関数 \(fg\) を計算できることがわかります。

合成関数の微分

関数 \(y = f(x)\) と \(z = g(y)\) の合成とは \(f\) を適用したあとに \(g\) を適用する関数、すなわち \(z = g(f(x))\) のことを指します。 ディープラーニングで用いるニューラルネットワークは、層を何層も重ねて複雑な関数を表現します。各々の層を 1 つの関数とみなすと、ニューラルネットワークは多くの関数（層）を合成した合成関数と見ることができます。 合成関数の微分を考える時には次に紹介する公式（合成関数の微分の公式）が有用です。 この公式は連鎖律 (chain rule) とも呼ばれています。 連鎖律は合成関数を微分を簡単に計算するための公式というだけではなく、ニューラルネットワークの訓練方法である誤差逆伝播法を理解する上で本質的な役割を果たします。

簡単な例として、

\[\left\{ (3x + 4)^{2} \right\}'\]

を計算することを考えます。 この式は、 \(3x+4\) という内側の部分と \((\cdot)^{2}\) という外側の部分で構成されています。 この式を \((9x^2 + 24x + 16)'\) のように展開してから微分を計算しても良いのですが、3乗や4乗とべき数が増えると式を展開するのが大変になります。 ここで役に立つ考え方が合成関数の微分です。 合成関数の微分は、内側の微分と外側の微分をそれぞれ行い、その結果をかけ合わせることで求めることができます。 外側の微分の際には関数の引数を入力とみなし、その入力についての微分を計算します。

それでは、具体的にこの \((3x+4)^2\) という関数の微分を考えてみます。 まず内側の関数を \(u = (3x+4)\) とおいて、

\[\left\{ (3x + 4)^{2} \right\}' = (u^{2})'\]

と見ます。ここで、 \((\cdot)'\) をもう少し厳密に考える必要が出てきます。 今変数は \(x\), \(u\) の2つあるため、 \((\cdot)'\) という表記では、 \(x\) で微分しているのか \(u\) で微分しているのかの区別がつきません。 そこで、多少複雑に見えますが、先程紹介した \(d\) を使った記法を用いて微分する変数を明示します。

合成関数の微分を公式としてまとめると次のようになります。

\[\frac{d}{dx} f(g(x)) = \frac{df(u)}{du}\frac{du}{dx}\]

ここで \(u = g(x)\) です。

公式を見るよりも実際の適用例を見た方が理解しやすいかも知れません。 合成関数の微分の公式を用いて、先程の \((3x+4)^2\) の微分を計算すると次のようになります。 2行目で合成関数の微分の公式を利用していることに注目してください。

\[\begin{split}\begin{aligned} \left\{ (3x + 4)^{2} \right\}' &= \frac{d}{dx} \left\{ (3x + 4)^{2} \right\} \\ &= \frac{du}{dx} \frac{d}{du} (u^2) \\ &= \frac{d}{dx} (3x + 4) \cdot \frac{d}{du} (u^{2}) \\ &= 3 \cdot 2u \\ &= 6u = 6(3x + 4) = 18x + 24 \\ \end{aligned}\end{split}\]

気になる人は、 \((3x + 4)^2\) を展開してから各項を微分した場合と結果が一致していることを確かめてみてください。

偏微分

機械学習では、1つの入力変数 \(x\) から出力変数 \(y\) を予測するケースは稀であり、多くの場合、複数の入力変数 \(x_1, x_2, \dots, x_M\) を用いて \(y\) を予測する多変数関数が扱われます。 例えば、家賃を予測する場合、部屋の広さだけではなく、駅からの距離や周辺の犯罪発生率なども同時に考慮した方がより正確に予測ができると期待されます。 複数の入力 \(x_1, x_2, \dots, x_M\) をとる関数 \(f(x_1, x_2, \dots, x_M)\) を多変数関数とよびます。 この多変数関数において、ある入力 \(x_m\) にのみ注目して微分することを 偏微分 とよび、

\[\frac{\partial}{\partial x_{m}} f(x_1, x_2, \dots, x_M)\]

と表します。微分を意味する記号が、 \(d\) から \(\partial\) に変わっています。こうすると、 \(\frac{\partial}{\partial x_m}\) は \(x_m\) 以外を定数と考え、 \(x_m\) にのみ着目して微分を行うという意味となります（注釈3）。

以下の例で具体的な計算の流れを確認しましょう。

\[\begin{split}\begin{aligned} \frac{\partial}{\partial x_1} \left( 3x_1+4x_2 \right) &= \frac{\partial}{\partial x_1} \left( 3x_1 \right) + \frac{\partial}{\partial x_1} \left( 4x_2 \right) \\ &= 3 \times \frac{\partial}{\partial x_1} \left( x_1 \right) + 4 \times \frac{\partial}{\partial x_1} x_2 \\ &= 3 \times 1 + 4 \times 0 \\ &= 3 \end{aligned}\end{split}\]

偏微分でも微分と同じ公式を適用できます。今回のケースでは、 \(x_1\) にだけ着目しており、 \(x_2\) は定数として扱かっています。そのため、上式の 2 行目から 3 行目で \(x_2\) を \(x_1\) で偏微分した値を \(0\) としています（定数の微分は \(0\) であったことを思い出してください）。

---

注釈 1

ここで考えている関数のグラフでは、グラフ上のどの点を取ってもその点で接する接線がただ1本だけ引ける状況を考えています。例えば関数のグラフが谷の部分で「尖った」形をしていると，谷の底で複数の接線が引けてしまいます。ここではそのようなケースは考えず、関数のグラフは図のような「滑らか」なカーブになっている場合をイメージしてください。

▲上へ戻る

注釈 2

今は関数のグラフの「谷」を考えましたが、「山」でも同様に接線の傾きが \(0\) となるため、ある点での接線の傾きが \(0\) だからと言って、必ずしも関数がその点で最小値をとるとは限りません。

▲上へ戻る

注釈 3

入力変数が他の入力変数と独立でない場合は定数と考えることはできません。しかし本資料ではそのようなケースは出てきません。

▲上へ戻る