単回帰分析と重回帰分析

本章では、基礎的な機械学習手法として代表的な単回帰分析と重回帰分析の仕組みを、数式を用いて説明します。 また次章では、本章で紹介した数式を Python によるプログラミングで実装する例も紹介します。本章と次章を通じて、数学とプログラミングの結びつきを体験して理解することができます。

本チュートリアルの主題であるディープラーニングの前に、単回帰分析と重回帰分析を紹介することには 2 つの理由があります。 1 つ目は、単回帰分析と重回帰分析の数学がニューラルネットワーク含めたディープラーニングの数学の基礎となるためです。 2 つ目は、単回帰分析のアルゴリズムを通して微分、重回帰分析のアルゴリズムを通して線形代数に関する理解を深めることができるためです。

機械学習手法は、教師あり学習 (supervised learning) 、教師なし学習 (unsupervised learning) 、強化学習 (reinforcement learning) に大別され、単回帰分析は教師あり学習に含まれます。 本チュートリアルで扱う多くの手法が教師あり学習です。

教師あり学習の中でも典型的な問題設定は 2 つに大別されます。 与えられた入力変数から、\(10\) や \(0.1\) といった実数値を予測する 回帰 (regression) と、「赤ワイン」、「白ワイン」といったカテゴリを予測する分類 (classification) の 2 つです。

単回帰分析は回帰を行うための手法であり、1 つの入力変数から 1 つの出力変数を予測します。 それに対し、重回帰分析は、複数の入力変数から 1 つの出力変数を予測します。 この両手法は教師あり学習であるため、訓練の際には、入力変数 \(x\) と目的変数 \(t\) がペアで準備されている必要があります。

回帰分析を行うアルゴリズムでは、以下の 3 ステップを順番に考えていきます。

• Step 1 : モデルを決める

• Step 2 : 目的関数を決める

• Step 3 : 最適なパラメータを求める

単回帰分析

問題設定（単回帰分析）

単回帰分析では、 1 つの入力変数から 1 つの出力変数を予測します。 今回は身近な例として、部屋の広さ \(x\) から家賃 \(y\) を予測する問題を考えてみます。

Step 1：モデルを決める（単回帰分析）

まずはじめに、入力変数 \(x\) と出力変数 \(y\) との関係をどのように定式化するかを決定します。 この定式化したものを モデル もしくは 数理モデル と呼びます。

単回帰分析におけるモデルを具体的に考えていきましょう。 例えば、家賃と部屋の広さの組で表されるデータを 3 つ集め、「家賃」を \(y\) 軸に、「部屋の広さ」を \(x\) 軸にとってそれらをプロットしたとき、次のようになっていたとします。

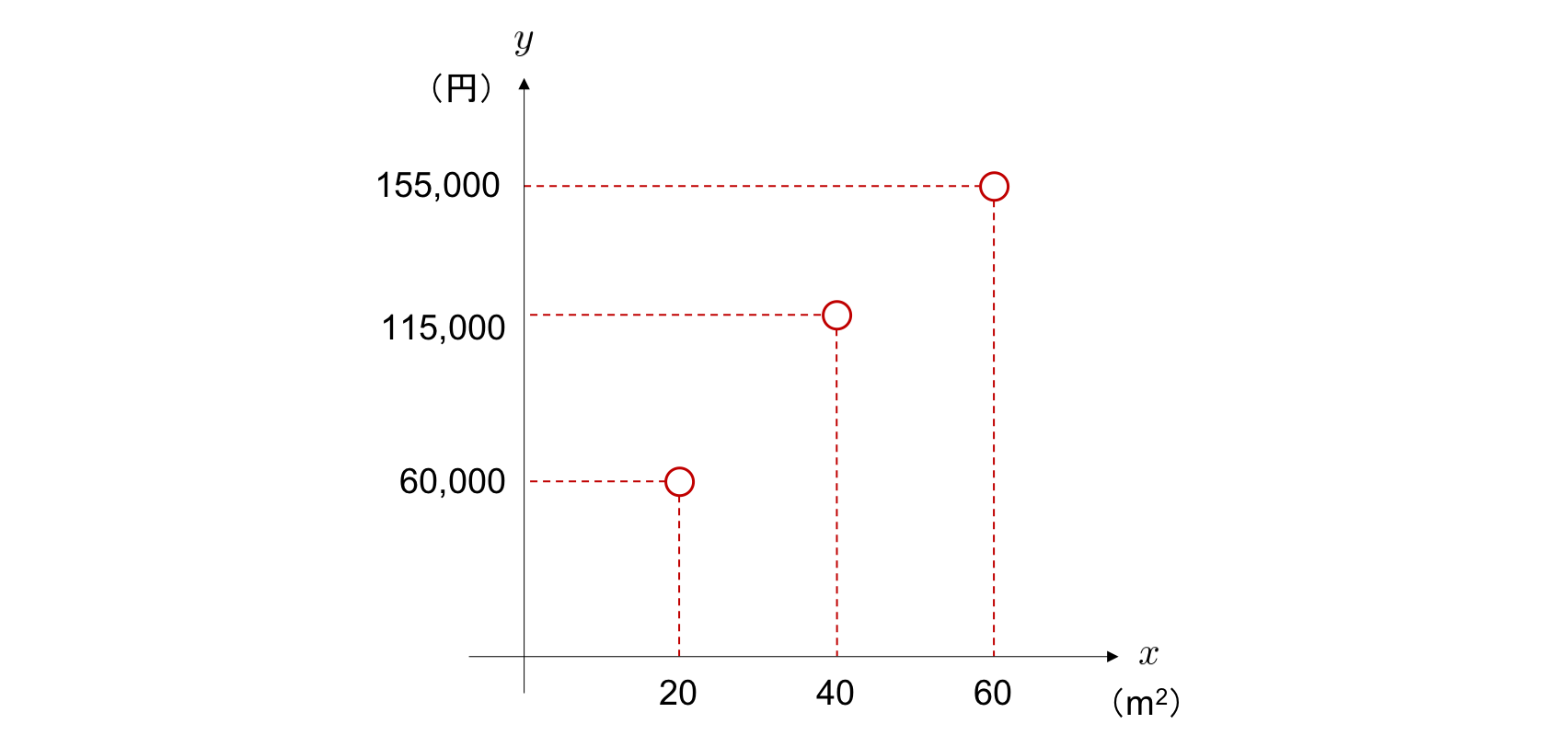
この場合、部屋が広くなるほど、家賃が高くなるという関係が予想されます。 また、この 2 変数間の関係性は直線によって表現を行うことができそうだと考えられます。 そこで、2 つのパラメータ \(w\) と \(b\) によって特徴づけられる直線の方程式

\[y = wx + b\]

によって、部屋の広さと家賃の関係を表すことを考えます。 ここで、\(w\) は 重み (weight) 、\(b\) は バイアス (bias) の頭文字を採用しています。

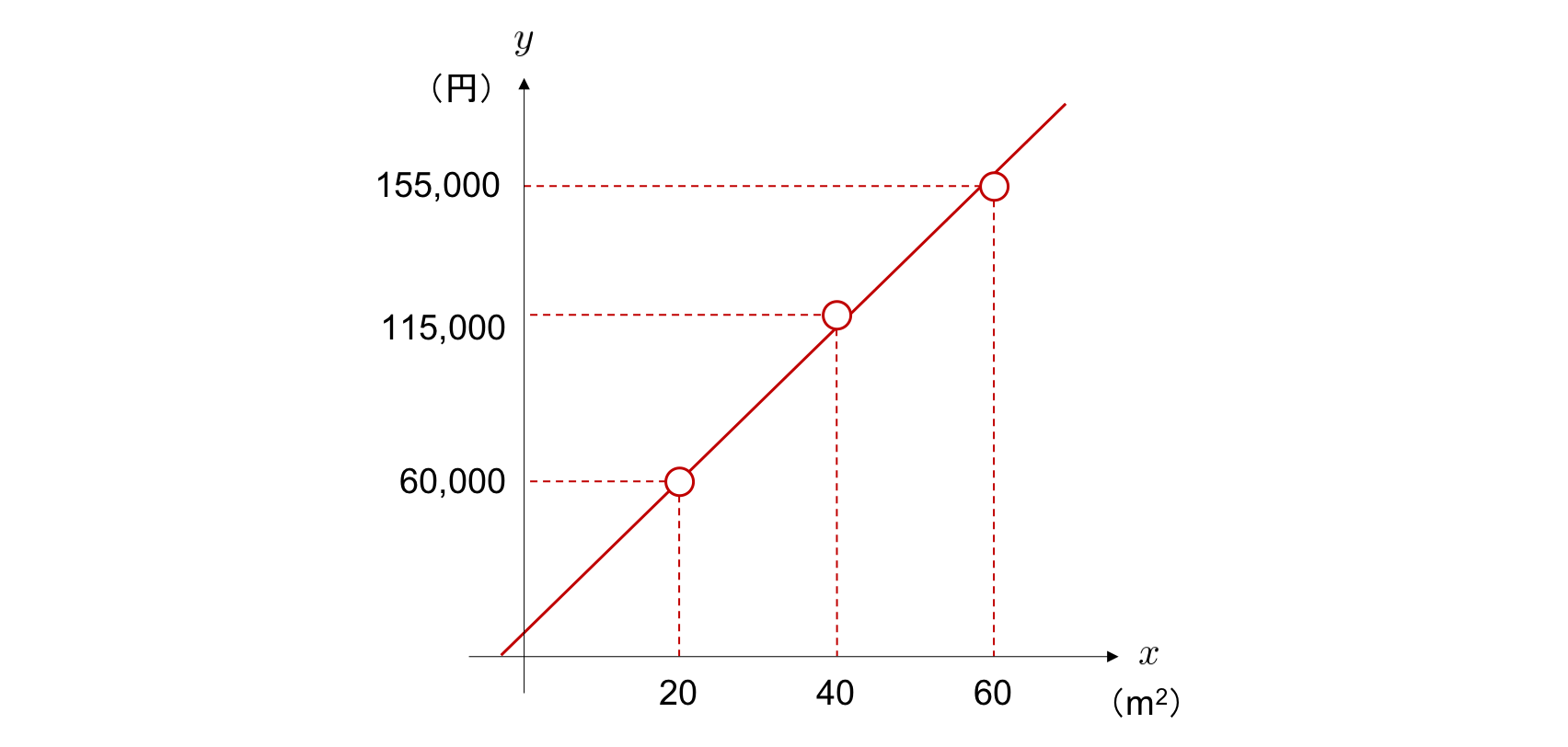
単回帰分析では、このようにモデルとして直線 \(y = wx + b\) を用います。 そして、2 つのパラメータ \(w\) と \(b\) を、直線がデータによくフィットするように調整します。

パラメータで特徴づけられたモデルを用いる場合、与えられた データセット に適合するように最適なパラメータを求めることが目標となります。 今回はデータセットとして部屋の広さ \(x\) と家賃 \(t\) の組からなるデータの集合を用います。 全部で \(N\) 個のデータがあり、\(n\) 番目のデータが \((x_n, t_n)\) と表されるとき、データセットは

\[\begin{split}\begin{align} \mathcal{D} &= \{(x_1, t_1), (x_2, t_2), \dots, (x_N, t_N)\} \\ &= \{(x_n, t_n)\}_{n=1}^{N} \end{align}\end{split}\]

と表すことができます（注釈1）。 これを用いて、新しい \(x\) を入力すると、それに対応する \(t\) を予測するモデルを訓練します。

前処理

次のステップに進む前に、データの前処理 (preprocessing) をひとつ紹介します。 データの 中心化 (centering) は、データの平均値が 0 になるように全てのデータを平行移動する処理を言います。 下図は、データ集合 \((x_n, y_n) \ (n=1,\dots,11)\) を、平均が \((0, 0)\) になるように平行移動する例です。

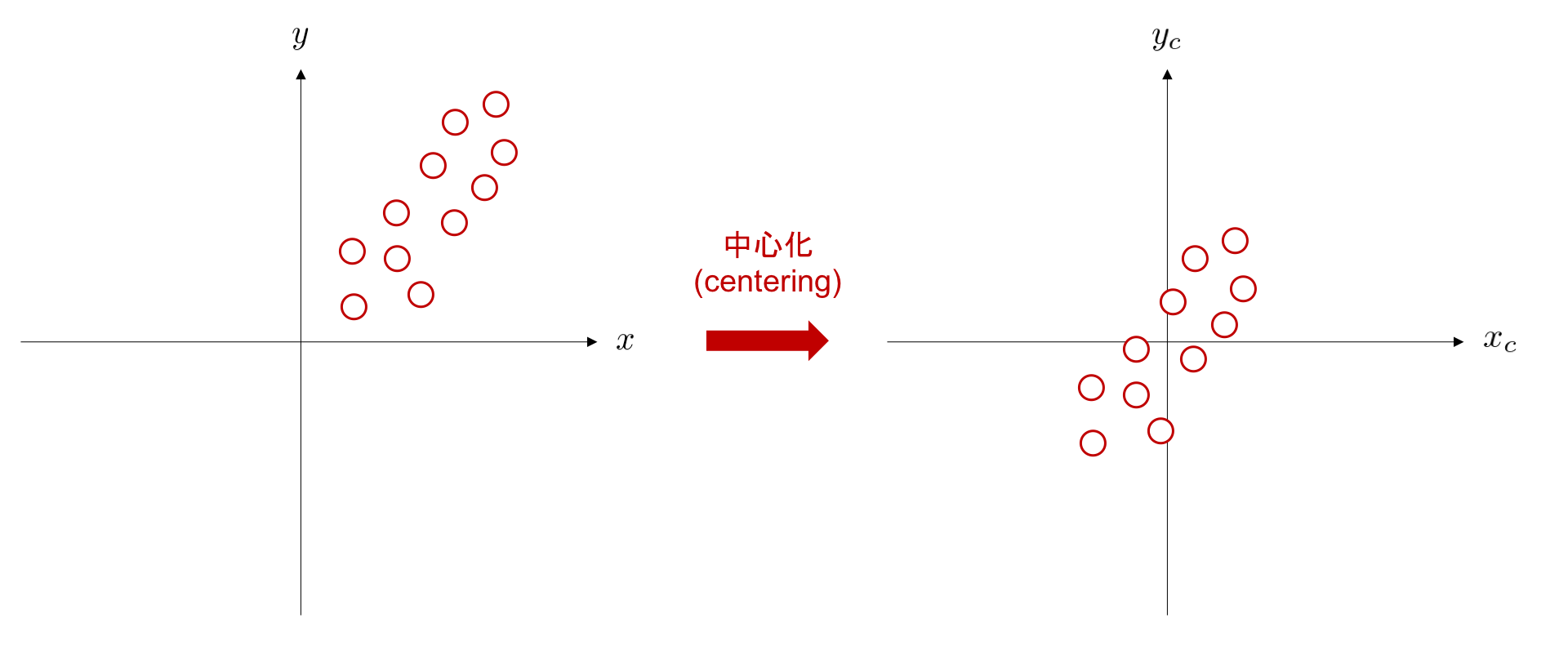
中心化によるデータ前処理の利点の一つとして、調整すべきパラメータを削減できることが挙げられます。中心化処理を行うことで切片を考慮する必要がなくなるため、データ間の関係性を表現する直線の方程式を、 \(y_c = wx_c\) のように、簡潔に表現可能となります。

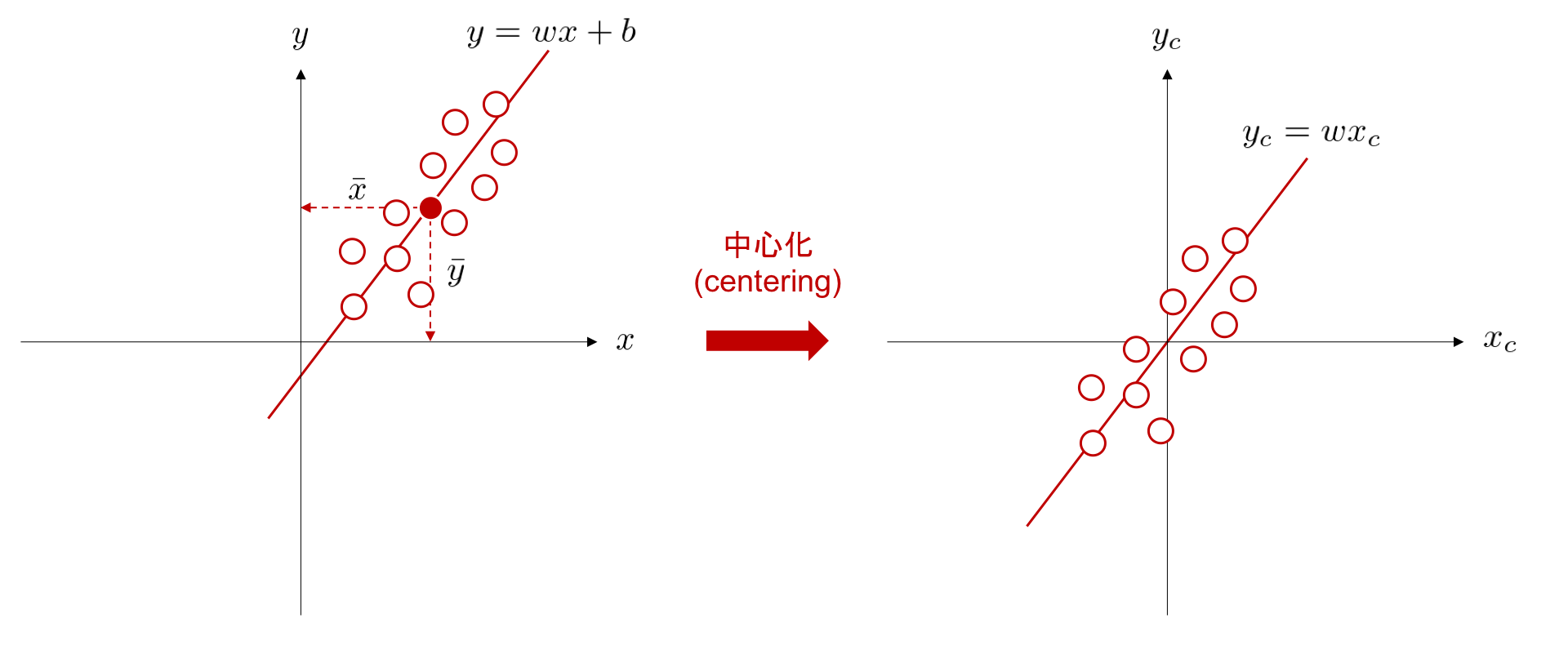
データセット内の入力変数と目的変数の平均をそれぞれ \(\bar{x}\), \(\bar{t}\) としたとき、中心化後の入力変数と目的変数は、

\[\begin{split}\begin{aligned} x_{c} &= x - \bar{x} \\ t_{c} &= t - \bar{t} \end{aligned}\end{split}\]

となります。

以降は記述を簡単にするため、\(_c\) という添え字を省略し、事前に中心化を行っている前提でデータを扱います。 また、そのデータにフィットさせたいモデルは、

\[y = wx\]

と、こちらも添え字 \(_c\) を省略して説明を行います。

Step 2：目的関数を決める（単回帰分析）

ここでの目標は、部屋の広さと家賃の関係を直線の方程式によってモデル化することです。 このために、予め収集されたいくつかのデータセットを使って、モデルが部屋の広さの値から予測した家賃（予測値）と、その部屋の広さに対応する実際の家賃（目標値）の差が小さくなるように、モデルのパラメータを決定します。

今回は、目的関数として こちらの章 ですでに紹介した予測値と目標値との二乗和誤差 (sum-of-squares error) を用います。 二乗和誤差が \(0\) のとき、またその時のみ予測値 \(y\) は目標値 \(t\) と完全に一致（\(t = y\)）しています。 \(n\) 個目のデータの部屋の広さ \(x_n\) が与えられたときのモデルの予測値 \(y_n\) と、対応する目標値 \(t_n\) との間の二乗誤差は、

\[(t_{n} - y_{n})^{2}\]

となります。これを全データに渡って合計したものが以下の二乗和誤差です。

\[\begin{split}\begin{aligned} L &= (t_1 - y_1)^2 + (t_2 - y_2)^2 + \cdots + (t_N - y_N)^2 \\ &= \sum_{n=1}^N (t_n - y_n )^2 \\ \end{aligned}\end{split}\]

今回用いるモデルは

\[y_{n} = wx_{n}\]

であるため、目的関数は

\[L = \sum_{n=1}^N (t_n - wx_n)^2\]

と書くこともできます。

Step 3：最適なパラメータを求める（単回帰分析）

この目的関数を最小化するようなパラメータを求めます。 ここで、目的関数は差の二乗和であり、常に正の値または \(0\) をとるような、下に凸な二次関数となっています。 （一般的には多くの場合において、最適なパラメータを用いてもモデルがすべてのデータを完全に表現できず、目的関数の値は \(0\) にはなりません。）

目的関数の値が最小となる点を求める際には、微分の知識が有用です。 微分では、対象とする関数の接線の傾きを求めることができます。凸関数では、この接線の傾きが 0 である点において、関数の最小値、もしくは最大値が得られます。 今回は、目的関数が \(x\) に関する二次関数となっているため、下図のように重み \(w\) に関する接線の傾きが \(0\) であるときに、目的関数の値が最小となります。

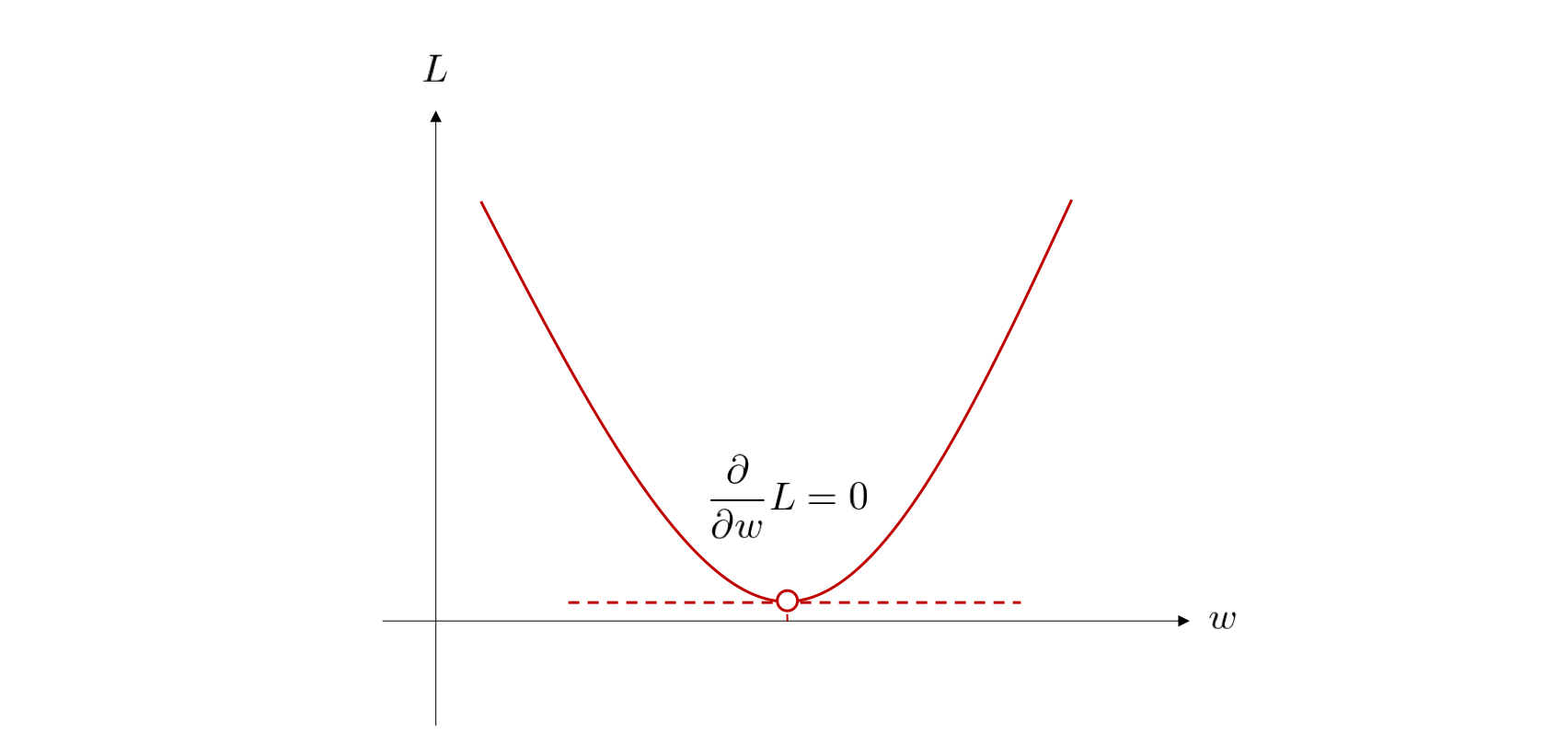
それでは、具体的に今回定めた目的関数 \(L\) をパラメータである \(w\) で微分してみましょう。 微分に関する基本的な計算や性質は こちらの章で紹介しました。

\[\frac{\partial}{\partial w} L = \frac{\partial}{\partial w} \sum_{n=1}^N (t_n - wx_n)^2\]

ここで、微分の線形性から、和の微分は、微分の和となるため、

\[\frac{\partial}{\partial w} L = \sum_{n=1}^N \frac{\partial}{\partial w} (t_n - wx_n)^2\]

と変形できます。

次に、総和（\(\sum\)）の中の各項に着目すると、

\[\frac{\partial}{\partial w} (t_n - wx_n)^2\]

となっており、この部分は \(t_n - wx_n\) と \((\cdot)^2\) という関数の合成関数になっています。 そこで、\(u_n = t_n - wx_n\)、\(f(u_n) = u_n^2\) とおいて計算すると、

\[\begin{split}\begin{aligned} \frac{\partial}{\partial w}(t_n - wx_n)^2 &= \frac{\partial}{\partial w} f(u_n) \\ &= \frac{\partial u_n}{\partial w}\frac{\partial f(u_n)}{\partial u_n} \\ &= -x_n (2 u_n) \\ &= -2x_n(t_n - wx_n) \end{aligned}\end{split}\]

が得られます。

これを \(\partial L / \partial w\) の式に戻すと、

\[\begin{split}\begin{aligned} \frac{\partial}{\partial w} L &= \sum_{n=1}^N \frac{\partial}{\partial w} (t_n - wx_n)^2 \\ &= -\sum_{n=1}^N 2x_n(t_n - wx_n) \end{aligned}\end{split}\]

となります。

この導関数の値が \(0\) となるときの \(w\) が、目的関数を最小にするパラメータです。 そこで、\(\frac{\partial}{\partial w} L = 0\) とおいてこれを \(w\) について解きます。

\[\begin{split}\begin{aligned} \frac{\partial}{\partial w} L &= 0 \\ -2 \sum_{n=1}^N x_n (t_n - wx_n) &= 0 \\ -2 \sum_{n=1}^N x_n t_n + 2 \sum_{n=1}^N wx^2_n &= 0 \\ -2 \sum_{n=1}^N x_n t_n + 2 w \sum_{n=1}^N x^2_n &= 0 \\ w \sum_{n=1}^N x^2_n &= \sum_{n=1}^N x_n t_n \\ \end{aligned}\end{split}\]

以上より、

\[w = \frac{\sum_{n=1}^N x_n t_n}{\sum_{n=1}^N x^2_n}\]

と求まりました。これを最適な \(w\) と呼びます。 この値は、与えられたデータセット \(\mathcal{D} = \{x_n, t_n\}_{n=1}^{N}\) のみから決定されています。

数値例

例題にあげていた数値でパラメータ \(w\) を求めてみましょう。

まずはデータの中心化を行うために、平均の値を事前に算出します。

\[\begin{split}\begin{aligned} \bar{x} &= \frac{1}{3} (20 + 40 + 60) = 40 \\ \bar{t} &= \frac{1}{3} (60000 + 115000 + 155000) = 110000 \end{aligned}\end{split}\]

この平均の値を使い、全変数に対して中心化を行うと、

\[\begin{split}\begin{aligned} x_{1} &= 20 - 40 = -20 \\ x_{2} &= 40 -40 = 0 \\ x_{3} &= 60- 40- = 20 \\ t_{1} &= 60000 - 110000 = -50000 \\ t_{2} &= 115000- 110000 = 5000 \\ t_{3} &= 155000 - 110000 = 45000 \end{aligned}\end{split}\]

となります。

これらの中心化後の値を用いて、最適なパラメータ \(w\) を計算すると、

\[\begin{split}\begin{aligned} w &= \frac{\sum_{n=1}^N x_n t_n}{\sum_{n=1}^N x_n^2} \\ &= \frac{x_1 t_1 + x_2 t_2 + x_3 t_3}{x_1^2 + x_2^2 + x_3^2} \\ &= \frac{-20 \times (-50000) + 0 \times 5000 + 20 \times 45000}{(-20)^2 + 0^2 + 20^2} \\ &= 2375 \end{aligned}\end{split}\]

と求まります。 したがって、家賃が　\(1\) m\(^{2}\) 増えるごとに、\(2375\) 円家賃が上昇しているとわかります。

この \(w\) を用いて決定される直線 \(y = 2375 x\) と、学習データとして用いた 3 つの点をプロットした図が以下です。

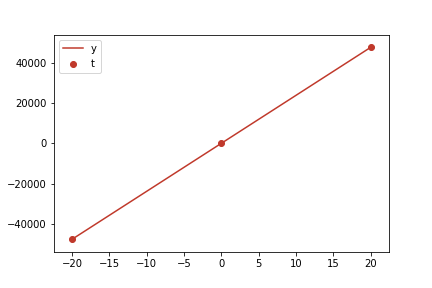
この直線上の点の \(y\) の値が、対応する \(x\) の値に対するここで訓練したモデルによる予測値です。 ここで、\(x\) 軸で負の値をとっていますが、これは中心化後であることに注意してください。

訓練済みのモデルを使って新しいサンプル \(x_{q}\) に対する家賃の予測を行います。 例えば、部屋の広さが 50 m\(^2\) の場合の家賃に対する予測値を計算する推論を行いましょう。

\[\begin{split}\begin{aligned} y_c &= wx_c \\ y_q - \bar{t} &= w(x_q - \bar{x}) \\ \Rightarrow y_q &= w(x_q - \bar{x}) + \bar{t} \\ &= 2375 (50 - 40) + 110000 \\ &= 133750 \end{aligned}\end{split}\]

このように、部屋の広さが　50 m\(^{2}\) の場合の家賃が 133,750 円であると予測することができました。 上記のように、モデル化の際に中心化を行っていた処理を推論の際には元に戻して計算しましょう。

重回帰分析

問題設定（重回帰分析）

重回帰分析も単回帰分析の場合と同様に家賃を予測する問題を題材にして説明します。 単回帰分析の場合と異なり、入力変数として「部屋の広さ」だけでなく、「駅からの距離」や「犯罪発生率」などの変数を合わせて考慮することにします。 部屋の広さを \(x_{1}\)、駅からの距離を \(x_{2}\)、…、犯罪発生率を \(x_{M}\) といった形で表し、\(M\) 個の入力変数を扱うことを考えてみましょう。

Step 1：モデルを決める（重回帰分析）

単回帰分析では、

\[y = wx + b\]

のように直線の方程式をモデルとして用いていました。重回帰分析でも、

\[y = w_{1}x_{1} + w_{2}x_{2} + \cdots + w_{M}x_{M} + b\]

のように、単回帰分析と似た形のモデルを定義します。 単回帰分析の際は二次元平面を考え、その平面上に存在するデータに最もよくフィットする直線を考えましたが、今回は \(M\) 次元空間に存在するデータに最もよくフィットする 直線を考えることになります。

重回帰分析のモデルは総和の記号を使って表記すると、

\[y = \sum_{m=1}^{M} w_{m} x_{m} + b\]

と書くことができます。

ここでバイアス \(b\) の扱い方を改めて考えます。 単回帰分析では、中心化を前処理として施し、バイアス \(b\) を省略することで、簡潔に定式化することができました。

重回帰分析では、 \(M\) 個の重み \(w_{1}, w_{2}, \dots, w_{M}\) と 1 個のバイアス \(b\) があり、合わせて \(M + 1\) 個のパラメータが存在します。これらのパラメータをうまく定式化することを考えます。 そこで、今回は \(x_0 = 1\)、\(w_0 = b\) とおくことで、

\[\begin{split}\begin{aligned} y &= w_{1}x_{1} + w_{2}x_{2} + \cdots + w_{M}x_{M} + b \\ &= w_{1}x_{1} + w_{2}x_{2} + \cdots + w_{M}x_{M} + w_{0}x_{0} \\ &= w_{0}x_{0} + w_{1}x_{1} + \cdots + w_{M}x_{M} \\ &= \sum_{m=0}^M w_{m} x_{m} \end{aligned}\end{split}\]

のように \(b\) を総和の内側の項に含めて、簡潔に表記できるようにします。 （ここで、 \(\sum\) 記号の下部が \(m=1\) ではなく \(m=0\) となっていることに注意してください。）

さらに、ここから線形代数で学んだ知識を活かして、数式を整理していきます。 上式をベクトルの内積を用いて表記しなおすと、

\[\begin{split}\begin{aligned} y &= w_{0}x_{0} + w_{1}x_{1} + \cdots + w_{M}x_{M} \\ &= \begin{bmatrix} w_{0} & w_{1} & \cdots & w_{M} \end{bmatrix} \begin{bmatrix} x_{0} \\ x_{1} \\ \vdots \\ x_{M} \end{bmatrix} \\ &= {\bf w}^{\rm T}{\bf x} \end{aligned}\end{split}\]

のように、シンプルな形式で表現することができます。 このモデルが持つパラメータは前述の通り \(M + 1\) 個あり、\(M + 1\) 次元のベクトル \({\bf w}\) で表されています。 重回帰分析では、この \({\bf w}\) のすべての要素について最適な値を求めます。

Step 2：目的関数を決める（重回帰分析）

単回帰分析の例と比べると、入力変数は増えましたが、家賃を目標値としている点は変わっていません。 そこで、単回帰分析と同じ目的関数

\[L = (t_1 - y_1)^2 + (t_2 - y_2)^2 + \cdots + (t_N - y_N)^2\]

を用います。 この目的関数は、ベクトルの内積を用いて表記し直すと、

\[\begin{split}\begin{aligned} L &= (t_1 - y_1)^2 + (t_2 - y_2)^2 + \cdots + (t_N - y_N)^2 \\ &= \begin{bmatrix} t_1 - y_1 & t_2 - y_2 & \cdots & t_N - y_N \end{bmatrix} \begin{bmatrix} t_1 - y_1 \\ t_2 - y_2 \\ \vdots \\ t_N - y_N \end{bmatrix} \\ &= ({\bf t} - {\bf y})^{\rm T}({\bf t} - {\bf y}) \end{aligned}\end{split}\]

と書くことができます。

ここで、内積には交換法則が成り立つため、\({\bf w}^{\rm T}{\bf x}\) は \({\bf x}^{\rm T}{\bf w}\) と書くこともできます。これを利用して、モデルの方程式 \({\bf y} = {\bf w}^{\rm T}{\bf x}\) を、以下のように変形します。

\[\begin{split}\begin{aligned} {\bf y} = \begin{bmatrix} y_1 \\ y_2 \\ \vdots \\ y_N \end{bmatrix} = \begin{bmatrix} {\bf x}_1^{\rm T}{\bf w} \\ {\bf x}_2^{\rm T}{\bf w} \\ \vdots \\ {\bf x}_N^{\rm T}{\bf w} \end{bmatrix} = \begin{bmatrix} {\bf x}_1^{\rm T} \\ {\bf x}_2^{\rm T} \\ \vdots \\ {\bf x}_N^{\rm T} \end{bmatrix} {\bf w} \end{aligned}\end{split}\]

さらに、\({\bf x}_n^{\rm T} = \bigl[ x_{n0},\ x_{n1},\ x_{n2},\ \dots,\ x_{nM} \bigr]\) \((n = 1, \dots, N)\) と展開すると、

\[\begin{split}\begin{aligned} {\bf y} &= \begin{bmatrix} x_{10} & x_{11} & x_{12} & \cdots & x_{1M} \\ x_{20} & x_{21} & x_{22} & \cdots & x_{2M} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ x_{N0} & x_{N1} & x_{N2} & \cdots & x_{NM} \end{bmatrix} \begin{bmatrix} w_{0} \\ w_{1} \\ w_{2} \\ \vdots \\ w_{M} \end{bmatrix} \\ &= {\bf X}{\bf w} \end{aligned}\end{split}\]

と表記できます。 ここで、\(N \times M\) 行列 \({\bf X}\) は、各行が各データを表しており、各列が各入力変数を表しています。 このような行列を、デザイン行列 (design matrix) と呼びます。 各列はそれぞれ入力変数の種類に対応しており、例えば、部屋の広さや、駅からの距離などです。

各行が表すデータ点がどのように表されているかを説明するため、具体的な数値例を挙げます。 部屋の広さ \(= 50{\rm m}^2\) 、駅からの距離 \(= 600 {\rm m}\) 、犯罪発生率 \(= 2\%\) という 3 つの入力変数を考える場合、\(M = 3\) であり、これが \(n\) 個目のデータのとき、\({\bf x}_n^{\rm T}\) は、

\[{\bf x}_n^{\rm T} = \begin{bmatrix} 1 & 50 & 600 & 0.02 \end{bmatrix}\]

となります。先頭に \(1\) があるのは、Step 1 で \(x_0 = 1\) と定めたためです。

Step 3：パラメータを最適化する（重回帰分析）

それでは、目的関数 \(L\) を最小化するモデルのパラメータベクトル \({\bf w}\) を求めましょう。 単回帰分析と同様に、目的関数をパラメータで微分して 0 とおき、\({\bf w}\) について解きます。

まずは目的関数に登場している予測値 \({\bf y}\) を、パラメータ \({\bf w}\) を用いた表記に置き換えます。

\[\begin{split}\begin{aligned} L &= ({\bf t} - {\bf y})^{\rm T} ({\bf t} - {\bf y}) \\ &= ({\bf t} - {\bf X}{\bf w})^{\rm T} ({\bf t} - {\bf X}{\bf w}) \\ &= \{ {\bf t}^{\rm T} - ({\bf X}{\bf w})^{\rm T} \} ({\bf t} - {\bf X}{\bf w}) \\ &= ({\bf t}^{\rm T} - {\bf w}^{\rm T}{\bf X}^{\rm T}) ({\bf t} - {\bf X}{\bf w}) \end{aligned}\end{split}\]

ここで、転置の公式 \(({\bf A}{\bf B})^{\rm T} = {\bf B}^{\rm T}{\bf A}^{\rm T}\) を用いました。

さらに分配法則を使って展開すると、

\[L = {\bf t}^{\rm T}{\bf t} - {\bf t}^{\rm T}{\bf X}{\bf w} - {\bf w}^{\rm T}{\bf X}^{\rm T}{\bf t} + {\bf w}^{\rm T}{\bf X}^{\rm T}{\bf X}{\bf w}\]

となります。この目的関数に対しパラメータの \({\bf w}\) についての偏微分を計算します。

その前に、この式をもう少し整理します。 まず、\((1)^{\rm T} = 1\) のように、スカラは転置しても変化しません。 また、\({\bf w} \in \mathbb{R}^{M+1}\)、\({\bf X} \in \mathbb{R}^{N \times (M+1)}\) であり、\({\bf X}{\bf w} \in \mathbb{R}^{N}\) となることから、\({\bf t} \in \mathbb{R}^{N}\) との間の内積 \({\bf t}^{\rm T}{\bf X}{\bf w} \in \mathbb{R}\) は、スカラになります。 したがって、

\[({\bf t}^{\rm T}{\bf X}{\bf w})^{\rm T} = {\bf t}^{\rm T}{\bf X}{\bf w}\]

が成り立ちます。

さらに、転置の公式 \(({\bf A}{\bf B}{\bf C})^{\rm T} = {\bf C}^{\rm T}{\bf B}^{\rm T}{\bf A}^{\rm T}\) より、

\[({\bf t}^{\rm T}{\bf X}{\bf w})^{\rm T} = {\bf w}^{\rm T} {\bf X}^{\rm T} {\bf t}\]

も成り立ちます。以上から、

\[({\bf t}^{T}{\bf X}{\bf w})^{T} = {\bf t}^{T}{\bf X}{\bf w} = {\bf w}^{T} {\bf X}^{T} {\bf t}\]

が導かれます。目的関数 \(L\) は、この式を利用して、

\[L = {\bf t}^{\rm T}{\bf t} - 2{\bf t}^{\rm T}{\bf X}{\bf w}+ {\bf w}^{\rm T}{\bf X}^{\rm T}{\bf X}{\bf w}\]

と変形できます。

ここで、\({\bf w}\) に関する偏微分を行いやすくするため、\({\bf w}\) 以外の定数項を一つにまとめます。

\[\begin{split}\begin{aligned} L &= {\bf t}^{\rm T}{\bf t} - 2{\bf t}^{\rm T}{\bf X}{\bf w} + {\bf w}^{\rm T}{\bf X}^{\rm T}{\bf X}{\bf w} \\ &= {\bf t}^{\rm T}{\bf t} - 2({\bf X}^{\rm T}{\bf t})^{\rm T} {\bf w} + {\bf w}^{\rm T}{\bf X}^{\rm T}{\bf X}{\bf w} \\ &= c + {\bf b}^{\rm T}{\bf w} + {\bf w}^{\rm T}{\bf A}{\bf w} \end{aligned}\end{split}\]

すると、\({\bf w}\) に関する二次形式で表現できました。 ここで、

\[\begin{split}\begin{align} {\bf A} &= {\bf X}^{\rm T}{\bf X} \\ {\bf b} &= -2 {\bf X}^{\rm T}{\bf t} \\ c &= {\bf t}^{\rm T}{\bf t} \end{align}\end{split}\]

とおいていることに注意してください。

それでは、目的関数を最小にするパラメータ \({\bf w}\) の求め方を考えます。 目的関数はパラメータ \({\bf w}\) に関して二次関数になっています。 まずは、\({\bf w}\) 以外のベクトルや行列に、具体的な数値を当てはめて考えてみましょう。 例えば、

\[\begin{split}{\bf w} = \begin{bmatrix} w_1 \\ w_2 \end{bmatrix}, {\bf A} = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}, {\bf b} = \begin{bmatrix} 1 \\ 2 \end{bmatrix}, c = 1\end{split}\]

とおきます。すると、目的関数の値は

\[\begin{split}\begin{aligned} L &= {\bf w}^{\rm T}{\bf A}{\bf w} +{\bf b}^{\rm T}{\bf w} + c \\ &= \begin{bmatrix} w_1 & w_2 \end{bmatrix} \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \begin{bmatrix} w_1 \\ w_2 \end{bmatrix} + \begin{bmatrix} 1 & 2 \end{bmatrix} \begin{bmatrix} w_1 \\ w_2 \end{bmatrix} + 1 \\ &= \begin{bmatrix} w_1 & w_2 \end{bmatrix} \begin{bmatrix} w_1 + 2w_2 \\ 3w_1 + 4w_2 \end{bmatrix} + w_1 + 2w_2 + 1 \\ &= w_1 (w_1 + 2w_2) + w_2 (3w_1 + 4w_2) + w_1 + 2w_2 + 1 \\ &= w_1^2 + 5 w_1 w_2 + 4 w_2^2 + w_1 + 2 w_2 + 1 \\ \end{aligned}\end{split}\]

となります。これを \(w_1, w_2\) に関して整理すると、

\[\begin{split}\begin{aligned} L &= w_1^2 + (5 w_2 + 1) w_1 + (4 w_2^2 + 2 w_2 + 1) \\ &= 4 w_2^2 + (5 w_1 + 2) w_2 + (w_1^2 + w_1 + 1) \end{aligned}\end{split}\]

となり、\(w_1, w_2\) それぞれについて二次関数になっていることが分かります。

目的関数 \(L\) を \(w_1\) の二次関数、\(w_2\) の二次関数と見たとき、\(L\) は、下図のような概形となっています。

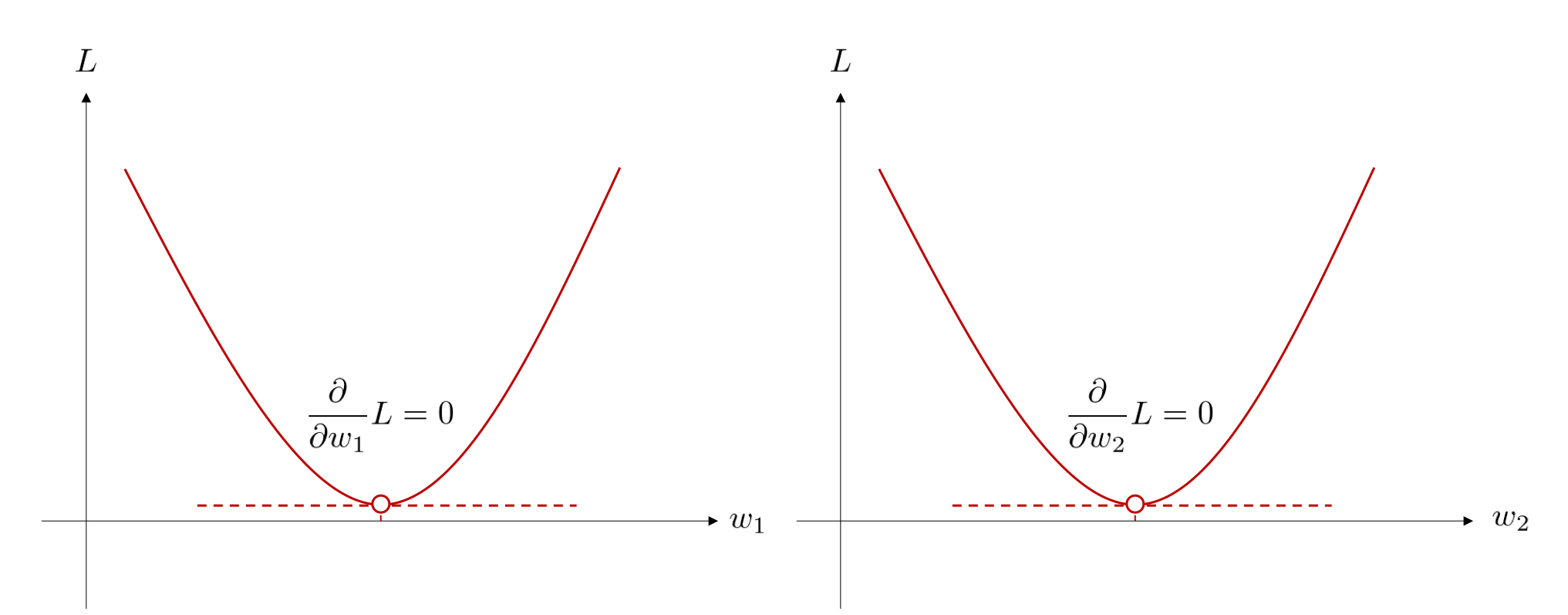
さらに、各次元が \(w_1, w_2, L\) を表す 3 次元空間上においては、 \(L\) の概形は下図のようになっています。

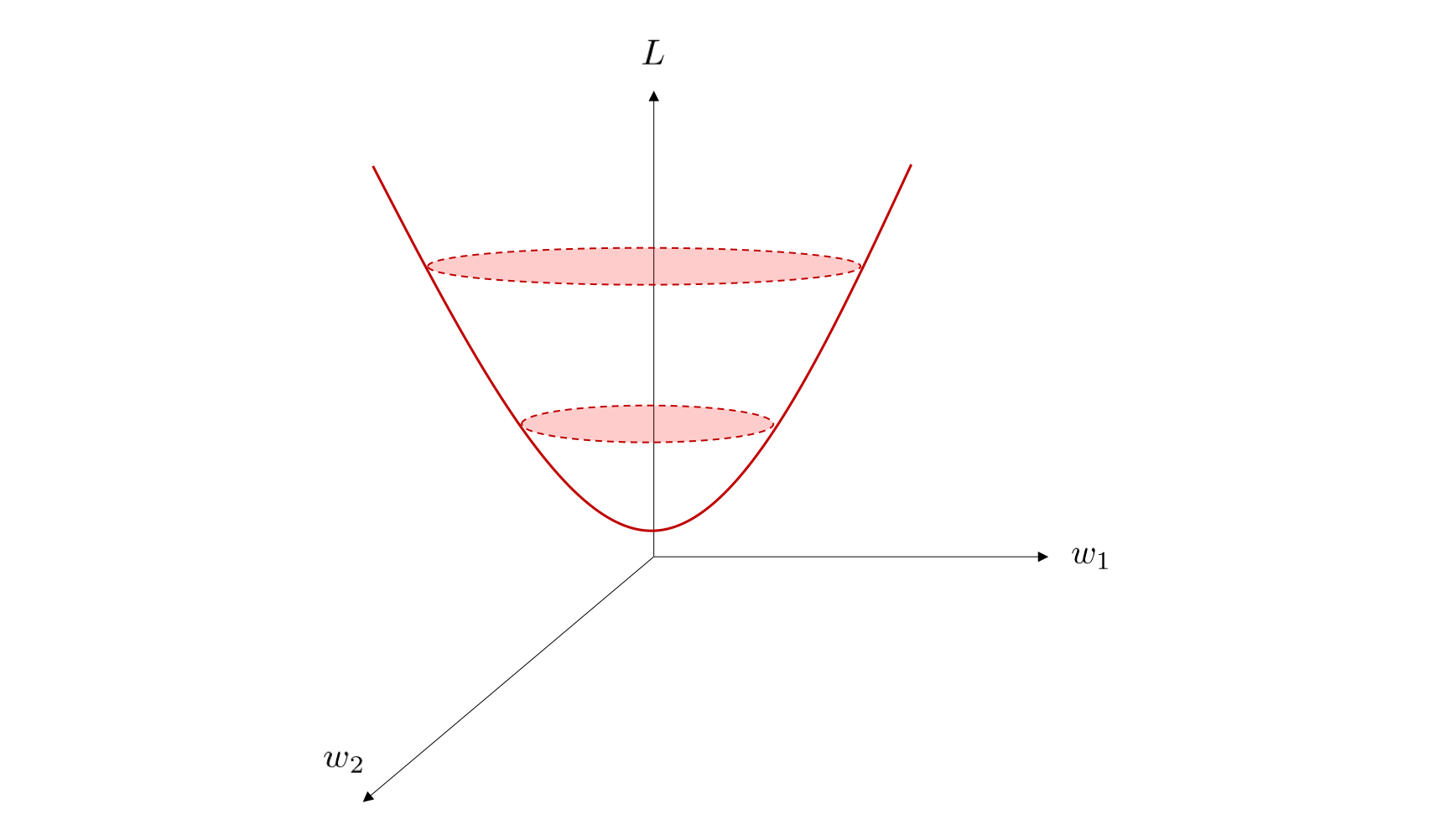
ここでは 2 つのパラメータ \(w_1\) と \(w_2\) について図示していますが、目的関数が 任意の \(M\) 個の変数 \(w_0, w_1, w_2, \dots, w_M\) によって特徴づけられている場合でも、目的関数がそれぞれのパラメータについて二次形式になっている限り、同様のことが言えます。 すなわち、\(M + 1\) 個の連立方程式、

\[\begin{split}\begin{cases} \frac {\partial }{\partial w_0}L = 0 \\ \frac {\partial }{\partial w_1}L = 0 \\ \ \ \ \ \ \vdots \\ \frac {\partial }{\partial w_M}L = 0 \\ \end{cases}\end{split}\]

を解けば良いということになります。 これはベクトルによる微分を用いて表記すると、以下のようになります。

\[\begin{split}\begin{aligned} \begin{bmatrix} \frac {\partial}{\partial w_0} L \\ \frac {\partial}{\partial w_1} L \\ \vdots \\ \frac {\partial}{\partial w_M} L \\ \end{bmatrix} &= \begin{bmatrix} 0 \\ 0 \\ \vdots \\ 0 \\ \end{bmatrix} \\ \Rightarrow \frac {\partial}{\partial {\bf w}} L &= {\bf 0} \\ \end{aligned}\end{split}\]

上式を \({\bf w}\) について解くために、以下のような式変形を行います。 式変形の途中で理解できない部分があった場合は、こちらの章 を読み返してみてください。 まずは、左辺について整理を行います。

\[\begin{split}\begin{aligned} \frac{\partial}{\partial {\bf w}} L &= \frac{\partial}{\partial {\bf w}} (c + {\bf b}^{\rm T}{\bf w} + {\bf w}^{\rm T}{\bf A}{\bf w}) \\ &=\frac{\partial}{\partial {\bf w}} (c) + \frac{\partial}{\partial {\bf w}} ({\bf b}^{\rm T}{\bf w}) + \frac{\partial}{\partial {\bf w}} ({\bf w}^{\rm T}{\bf A}{\bf w}) \\ &={\bf 0} + {\bf b}^{\rm T} + {\bf w}^{\rm T}({\bf A} + {\bf A}^{\rm T}) \end{aligned}\end{split}\]

これを \(0\) とおき、\({\bf A}\) 、\({\bf b}\) を展開すると

\[\begin{split}\begin{aligned} -2({\bf X}^{\rm T}{\bf t})^{\rm T} + {\bf w}^{\rm T} \{ {\bf X}^{\rm T}{\bf X} + ({\bf X}^{\rm T}{\bf X})^{\rm T} \} &= {\bf 0} \\ -2{\bf t}^{\rm T}{\bf X} + 2{\bf w}^{\rm T}{\bf X}^{\rm T}{\bf X} &= {\bf 0} \\ {\bf w}^{\rm T}{\bf X}^{\rm T}{\bf X}& = {\bf t}^{\rm T}{\bf X} \\ \end{aligned}\end{split}\]

のように式変形できます。

ここで両辺を転置して、 \({\bf w}^{\rm T}\) の転置を直しておきましょう。

\[\begin{split}\begin{aligned} ({\bf w}^{\rm T}{\bf X}^{\rm T}{\bf X}) ^{\rm T} & = ({\bf t}^{\rm T}{\bf X}) ^{\rm T} \\ {\bf X}^{\rm T}{\bf X}{\bf w} & = {\bf X}^{\rm T}{\bf t} \\ \end{aligned}\end{split}\]

ここで、\({\bf X}^{\rm T}{\bf X}\)に逆行列が存在すると仮定して、両辺に左側から \(({\bf X}^{\rm T}{\bf X})^{-1}\) を掛けると、

\[\begin{split}\begin{aligned} ({\bf X}^{\rm T}{\bf X})^{-1} {\bf X}^{\rm T}{\bf X} {\bf w} &= ({\bf X}^{\rm T}{\bf X})^{-1} {\bf X}^{\rm T}{\bf t} \\ {\bf I}{\bf w} &= ({\bf X}^{\rm T}{\bf X})^{-1} {\bf X}^{\rm T}{\bf t} \\ {\bf w} &= ({\bf X}^{\rm T}{\bf X})^{-1}{\bf X}^{\rm T}{\bf t} \end{aligned}\end{split}\]

が導かれます。特に、この最後の式を正規方程式 (normal equation) と呼びます。 上式は、与えられたデータを並べたデザイン行列 \({\bf X}\) と、各データの目標値を並べたベクトル \({\bf t}\) から、最適なパラメータ \({\bf w}\) を計算しています。 \({\bf I}\) は単位行列を表します。

\({\bf w}\) を求める際に気をつけたいこととして、以下の誤った式変形をしてしまう例が挙げられます。

\[\begin{split}\begin{aligned} {\bf X}^{\rm T}{\bf X}{\bf w} &= {\bf X}^{\rm T}{\bf t} \\ ({\bf X}^{\rm T})^{-1} {\bf X}^{\rm T}{\bf X}{\bf w} &= ({\bf X}^{\rm T})^{-1} {\bf X}^{\rm T}{\bf t} \\ {\bf X}{\bf w} &= {\bf t} \\ {\bf X}^{-1}{\bf X}{\bf w} &= {\bf X}^{-1}{\bf t} \\ {\bf w} &= {\bf X}^{-1}{\bf t} \end{aligned}\end{split}\]

上記の式変形は一般には成立しません。 この式変形が可能かどうかは、\({\bf X}^{-1}\) が存在するかどうか、に関わっています。 サンプルサイズ \(N\) と独立変数の数 \(M + 1\) が等しくない場合、\({\bf X} \in \mathbb{R}^{N \times (M + 1)}\) は正方行列ではないため、逆行列 \({\bf X}^{-1}\) を持ちません。 従って、上式の 2 行目の変形を行うことはできません（逆行列が求まるためのより厳密な条件についてはここでは省略します）。

一方、 \({\bf X}^{\rm T}{\bf X}\) は \((M + 1) \times (M + 1)\) 行列であり、その形はサンプルサイズ \(N\) に依存することなく、常に正方行列となるため、これを利用して式変形を行います。

新しい入力変数の値 \({\bf x}_q = [x_1, \dots, x_M]^{\rm T}\) に対して、対応する目標値 \(y_q\) を予測するためには、訓練により決定されたパラメータ \({\bf w}\) を用いて、

\[y_q = {\bf w}^{\rm T}{\bf x}_q\]

のように計算します。

---

注釈 1

データセット中の各データのことをデータ点（datum）ということがあります。具体的には、上の説明で同上した \(\mathcal{D}\) 中の各 \((x_1, t_1)\) などのことです。

▲上へ戻る