ニューラルネットワークの基礎¶
ニューラルネットワークとは¶
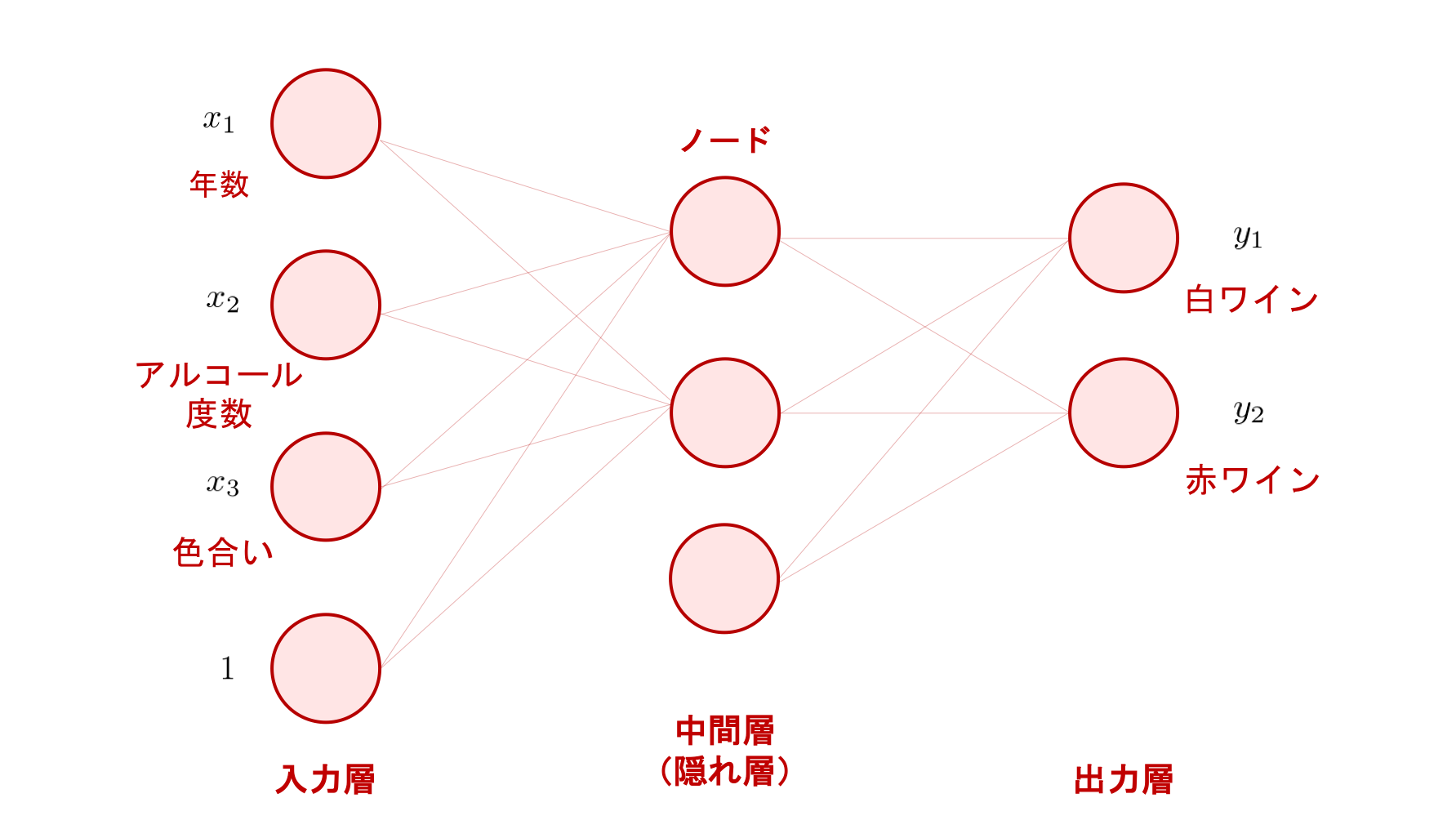
ニューラルネットワークは、微分可能な変換を繋げて作られた計算グラフ (computational graph) です。 本章では、まずは下の図のような、円で表されたノード (node) に値が入っていて、ノードとノードがエッジ (edge) で繋がれているようなものを考えます。
この図でいうノードの縦方向の集まりのことを層 (layer) と呼びます。 そしてディープラーニング (deep learning) とは、層の数が非常に多いニューラルネットワークを用いた機械学習の手法や、その周辺の研究領域のことを指します。
層（layer）¶
上の図は、ニューラルネットワークを用いて、ワインに関するいくつかの情報から、そのワインが「白ワイン」なのか「赤ワイン」なのか、というカテゴリを予測する分類問題を解く例を表しています。
左側から、最初の層を入力層 (input layer)、最後の層を出力層 (output layer)といい、その間にある層は中間層 （intermediate layer) もしくは隠れ層 (hidden layer) といいます。 上のニューラルネットワークは、入力層、中間層、出力層がそれぞれ一つずつあるので、合計 3 層の構造（アーキテクチャ; architecture）となっています。複数の中間層を持たせれば、さらに多層のニューラルネットワークとすることができます。
ニューラルネットワークは、層から層へ、値を変換していきます。 そのため、ニューラルネットワークとはこの変換がいくつも連なってできる一つの大きな関数だと考えることができます。 従って、基本的には、入力を受け取って、何か出力を返すものです。 そして、どのようなデータを入力し、どのような出力を作りたいかによって、入力層と出力層のノード数が決定されます。
上の例では、入力変数 \(x_1\) に年数、\(x_2\) にアルコールの度数、\(x_3\) に色合い、といったあるワインを表す定量的な情報が与えられています。 そのため、入力層のノードの数は入力変数の数 \(M\) （上の図では、\(M = 3\)）によって決定されます。 ここで、層と層の間にあるノード間の結合は、一つ一つが重みを持っており、上のような全結合型ニューラルネットワークの場合は、それらの重みをまとめて、一つの行列で表現します。 この際、単回帰分析と重回帰分析 の章で解説した重回帰分析の例と同じように、バイアスをその重み行列に含めて扱うため、入力層の最後に常に \(1\) を持つノードが追加されていることに注意してください。 このため、図では入力層のノード数が \(M + 1 = 3 + 1 = 4\) 個となっています。
また、今回はワインの情報を入力して、それが「赤ワイン」か「白ワイン」かを予測するという場合を表しているので、カテゴリ数が 2 の分類問題と言えます。 そのため、出力層のノード数は 2 となっています。 この出力層のノード数を変化させれば、3 つや 4 つのカテゴリ数の分類問題にも対応することができます。 また、離散的なカテゴリではなく、連続的な実数値を予測する回帰問題の場合は、目標値の種類に合わせて出力層のノード数を決定します。
構造（architecture）¶
下の図のように、層数が同じでも、中間層のノード数を 3 にするか、 5 にするか、などには任意性があります。 こういった値をどのように決めるかは、ニューラルネットワークを設計する人に委ねられています。 また、中間層自体をいくつ重ねるか、その個数も自分で決める必要があります。 こういった自分で決定するパラメータを、ハイパーパラメータと呼びます。
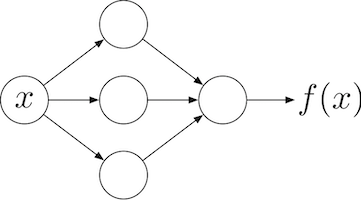中間層のノード数が 3 の場合
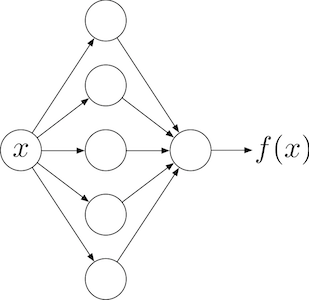中間層のノード数が 5 の場合
色々な種類（type）¶
ニューラルネットワークには、上図のような層間のノードが互いに密に結合した全結合型 (fully-connected) のものだけでなく、画像処理などでよく用いられる畳み込み型 (convolutional) のもの、系列データの扱いによく用いられる再帰型 (recurrent) のものなど、いくつもの種類があります。 また、基本的にそれらの違いは層間の結合の仕方にあり、別々の層間には別々の種類の結合の仕方を用いることができます。 つまり、1 つのニューラルネットワークの中に複数の種類の結合が混ざって現れることもあります。 例えば、入力に近いところでは畳み込み型の結合を用い、出力に近いところでは全結合型の結合を用いる、といったことがよく行われています。
本章では、まず最も基本となる全結合型のみに着目して、解説を行います。 その他の種類については、後の章で解説を行います。
ニューラルネットワークの計算¶
基本的な計算の流れ¶
それでは、「ワインの分類」を題材に、ニューラルネットワークにある入力が与えられたとき、どのように計算結果が得られ、その結果をどう使えば分類が行えるのかを、まずは数式を用いず、以下の図を見ながら理解しましょう。
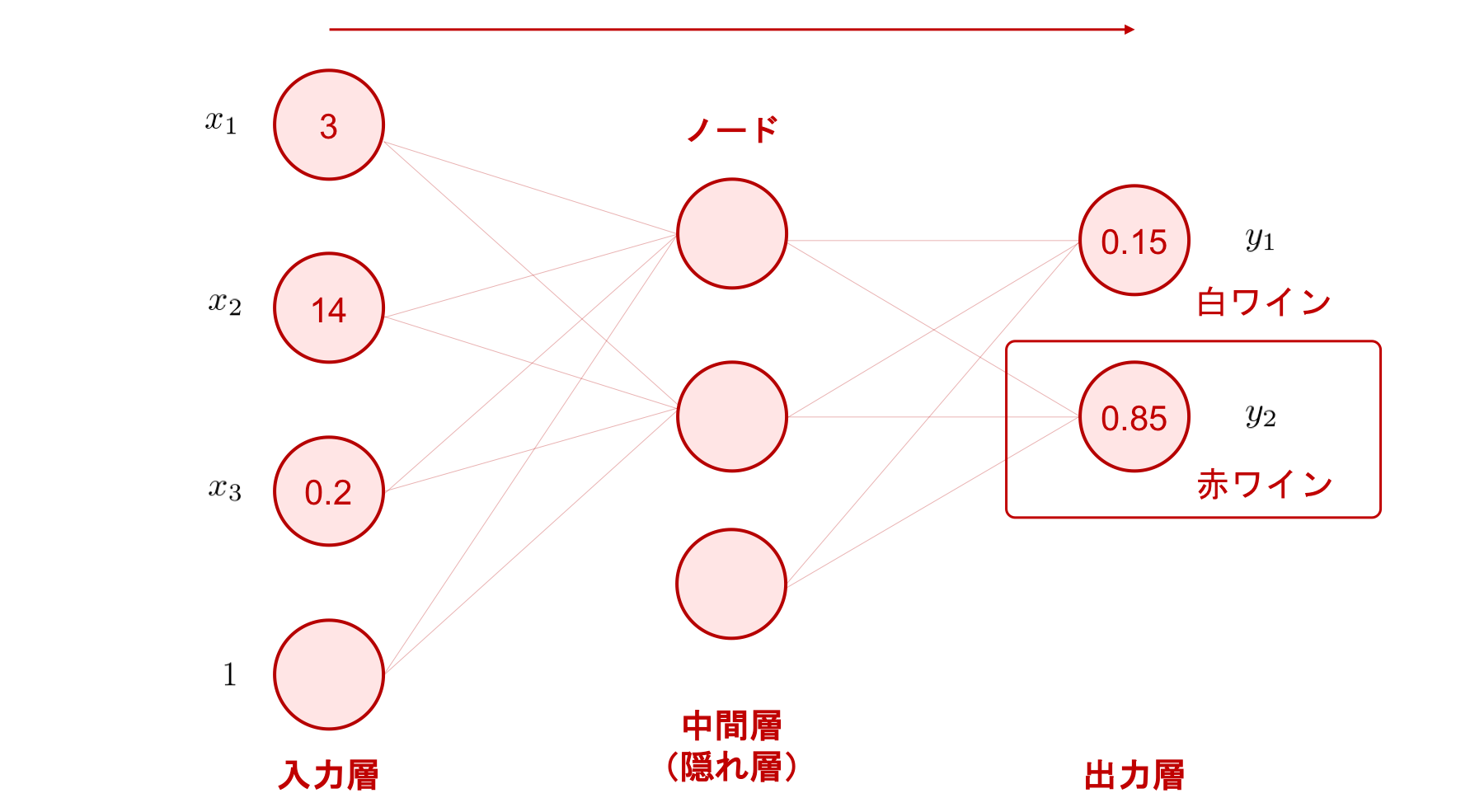
例えば、年数が 3 年、アルコール度数が 14 度、色合いが 0.2 で表されるワインがあるとします。
このワインの情報をニューラルネットワークの入力層に与えたところ、そこから中間層、そして出力層へと順番に計算が進み、最終的に \(y_1 = 0.15, y_2= 0.85\) という 2 つの数値が得られたとします。
この 2 つの数値は、入力されたワインが「赤ワイン」「白ワイン」という 2 つのカテゴリのそれぞれに属する確率を表しています。 分類問題では、出力された数値のうちどのノードが最も大きな値を持っているかによって、ニューラルネットワークの予測が決まります。 今回は、2 つの出力のうち \(y_{2}=0.85\) が最も大きな値となっているため、\(y_2\) に対応する「赤ワイン」が予測されたカテゴリとなります。
このように、入力が与えられたとき、ニューラルネットワークの各層を順番に計算していき、出力まで計算を行うことを、順伝播 (forward propagation) と言います。
それでは、ここからはこのような計算がニューラルネットワークの内部でどのように行われているのか、詳しく見ていきましょう。 ポイントは、ニューラルネットワークの各層では、前の層の出力値に「線形変換」と「非線形変換」を順番に施している、というところです。 それでは、線形変換とは何か、非線形変換とは何か、を順番に説明します。
線形変換¶
線形変換（注釈1）とは、入力ベクトルを \({\bf h}_0\) としたとき（注釈2）、重み行列 \({\bf W}_{10}\) と、バイアスベクトル \({\bf b}_1\) の 2 つを使って、次のような変換を行うことを言います。
これを踏まえて、以下の 2 層の全結合型ニューラルネットワークの図を見てみましょう。
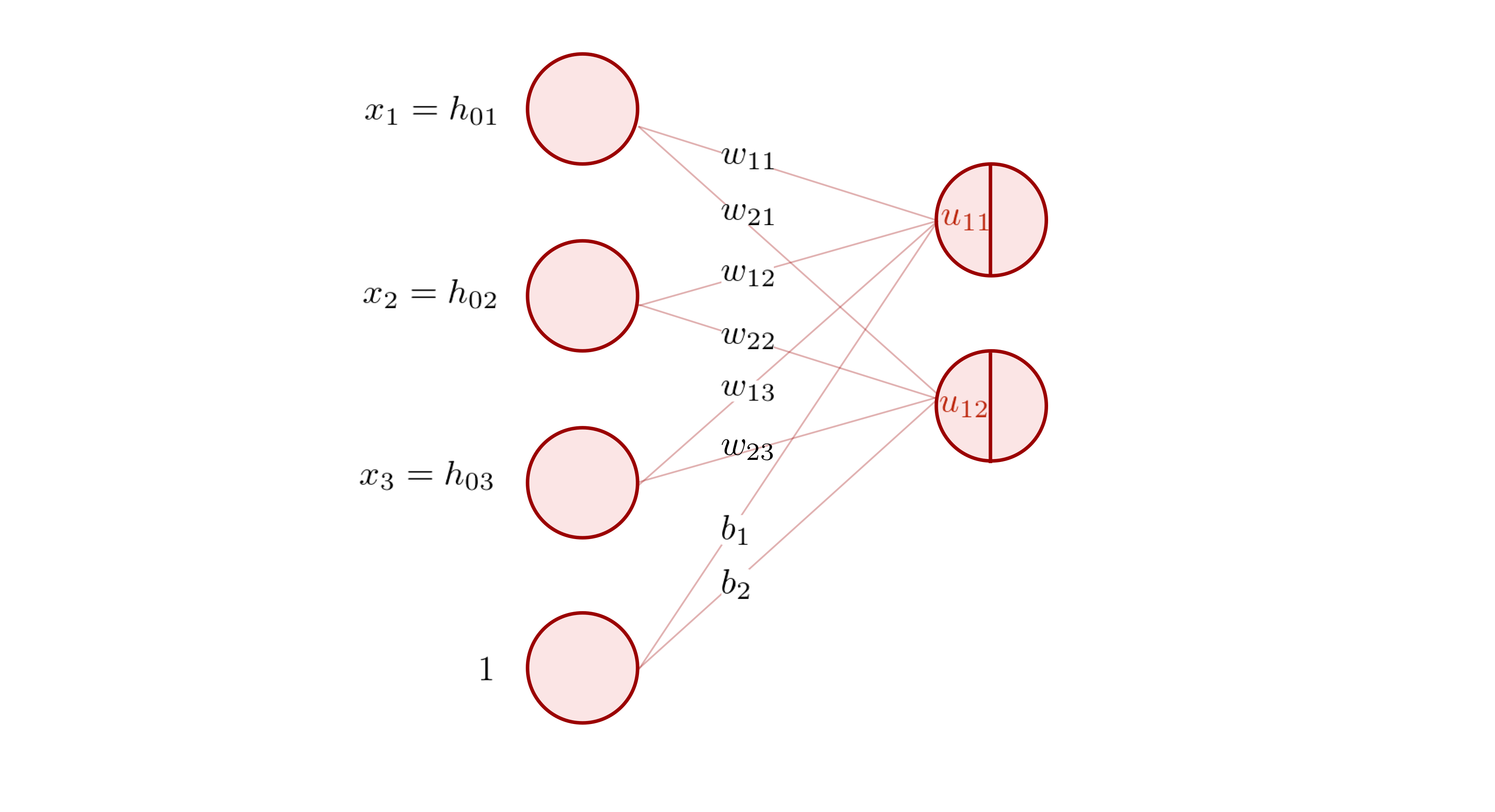
このニューラルネットワークは、上の式と同じ計算を行います。 2 つの層の間にはノードとノードを接続する線（エッジ）が書かれています。 そして、エッジの上には、\(w_{11}, w_{21}, \dots\) といった文字が書かれています。 これらは両端のノード間の結合重み (connection weight) を表しています。
入力層のノードが持つ値は、結合重みと掛け合わされ、出力層のノードに伝わります。出力層の 1 つのノードには、複数のノードから計算結果が伝わってくるので、これらを全部足し合わせます。
具体的には、以下のような計算をします。
この式は、入力ベクトル \({\bf h}_0\)、重み行列 \({\bf W}_{10}\)、バイアスベクトル \({\bf b}_1\)、および出力 \({\bf u}_1\) を
と定義すれば、
と書くことができ、本節の冒頭に示した式と一致していることが分かります。
以上から、全結合型ニューラルネットワークでは、層と層の間で線形変換が行われていることが分かりました。 ここで、出力層のノードを改めて見てみましょう。 ノードは真ん中に線が引かれて左右に分割されており、先程計算した出力値 \(u_{11}, u_{12}\) はその左側の半円の中に書かれています。
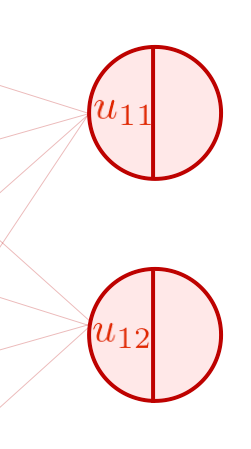
ニューラルネットワークの隠れ層では、一つ前の層に線形変換を適用した結果を受け取り、そこへさらに非線形変換を適用したものを出力します。 その結果を、この右側の半円の中に書き入れます。
次に、その非線形変換とは何なのか、またなぜ必要なのか説明していきます。
非線形変換¶
前節で紹介した線形変換のみでは、下図左のような入出力間が線形な関係性はよく近似することができるとしても、下図右のような入出力間が非線形な関係になっている場合には、観測データをうまく近似することができません。
例えば、線形変換のみで下図右の白い丸で表される観測データから \(x\) と \(y\) の関係を近似した場合、点線のような直線が得られたとします。 これでは、一部のデータについてはあまりよく当てはまっていないのが分かります。 しかし、もし \(xy\) 平面上で下図右の実線のような曲線を表現することができれば、より良く近似できるかもしれません。
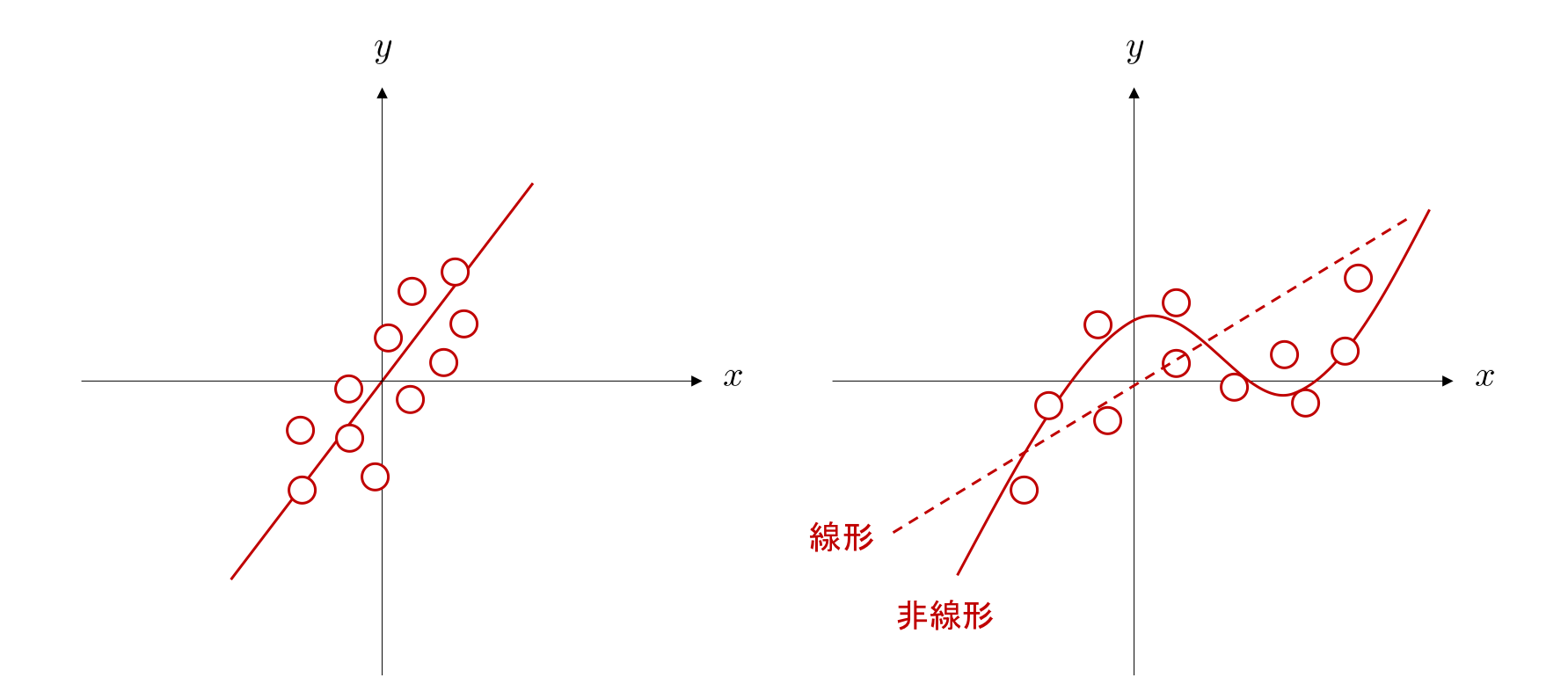
このようなケースに対応できるよう、ニューラルネットワークでは各層において、線形変換に続いて非線形変換を施し、層を積み重ねて作られるニューラルネットワーク全体としても非線形性を持つことができるようにしています。
そして、この非線形変換を行う関数のことを、ニューラルネットワークの文脈では活性化関数 (activation function) と呼びます。
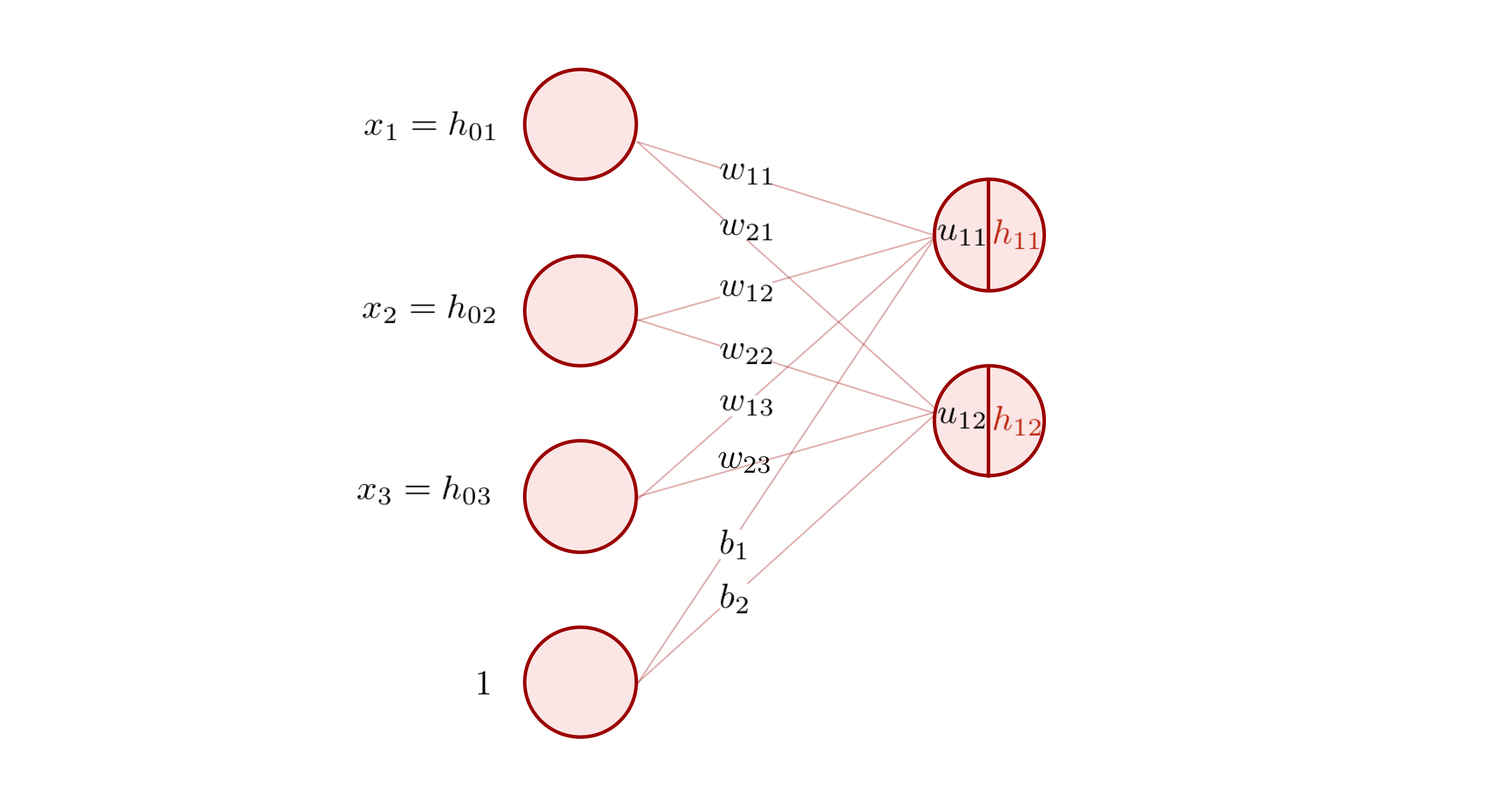
線形変換の節で用いた例に戻って、説明を進めます。 線形変換を行った結果 \(u_{11}, u_{12}\) のそれぞれに活性化関数 \(a\) を用いて非線形変換を行い、その結果を \(h_{11}, h_{12}\) とおきます。つまり、
です。 これらは活性値（activation）と呼ばれ、もしもう一つ層が続いているならば、次の層に渡される入力の値となります。
ロジスティックシグモイド関数¶
活性化関数の具体例としては、下図に示す ロジスティックシグモイド関数 (logistic sigmoid function) が従来、よく用いられてきました。
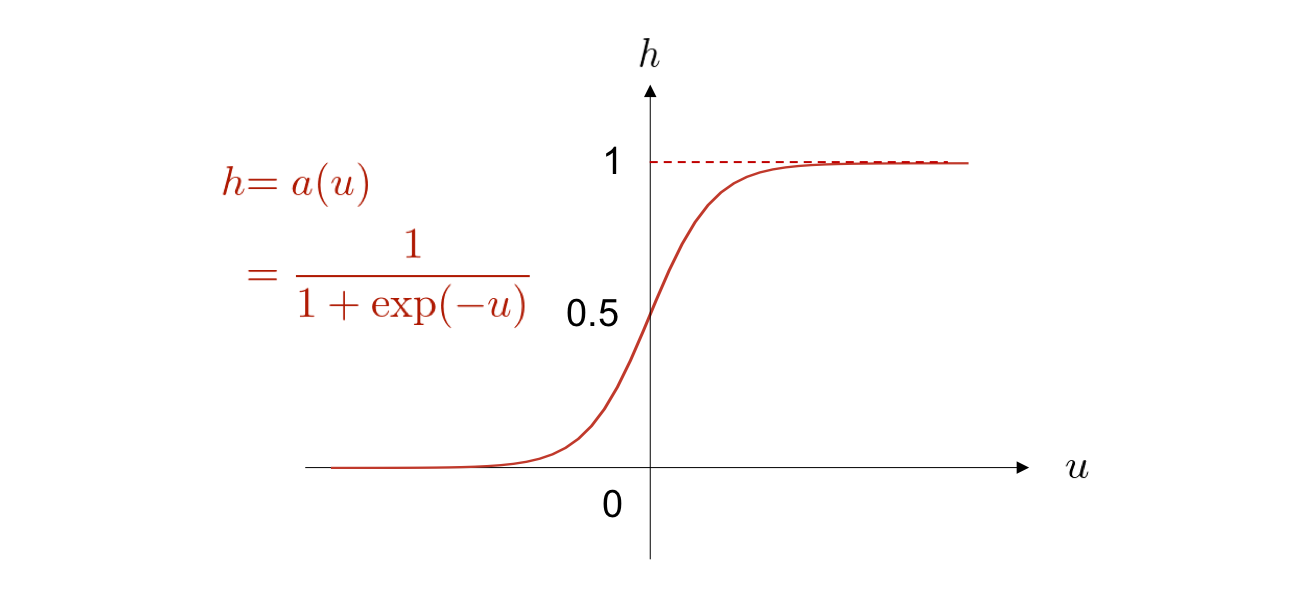
以下、シグモイド関数と呼びます。
しかし近年、層の数が多いニューラルネットワークではシグモイド関数は活性化関数としてほとんど用いられません。 その理由の一つは、シグモイド関数を活性化関数に採用すると、勾配消失 (vanishing gradient) という現象によって学習が進行しなくなる問題が発生しやすくなるためです。 この問題の詳細は本章の最後で紹介します。
ReLU¶
この問題を回避するために、最近では正規化線形関数 (ReLU: rectified linear unit) がよく用いられています。 これは、以下のような関数です。
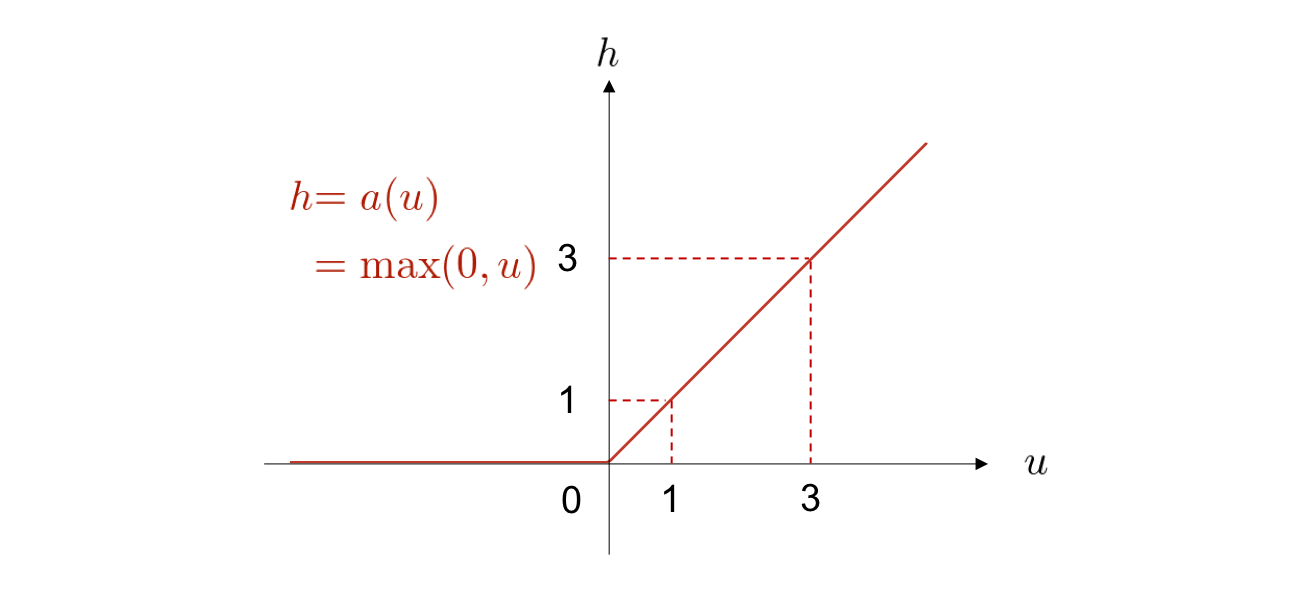
\(\max(0, u)\) は、\(0\) と \(u\) を比べて大きな方を返す関数です。 すなわち、ReLU は入力が負の値の場合には出力は 0 で一定であり、正の値の場合は入力をそのまま出力するという関数です。 シグモイド関数では、入力が \(0\) から離れた値をとると、どんどん曲線の傾き（勾配）が小さくなっていき、平らになっていくことが一つ前の図からも見て取れます。 それに対し、ReLU 関数は入力の値が正であれば、いくら大きくなっていっても、傾き（勾配）は一定です。 これが後ほど紹介する勾配消失という問題に有効に働きます。
数値を見ながら計算の流れを確認¶
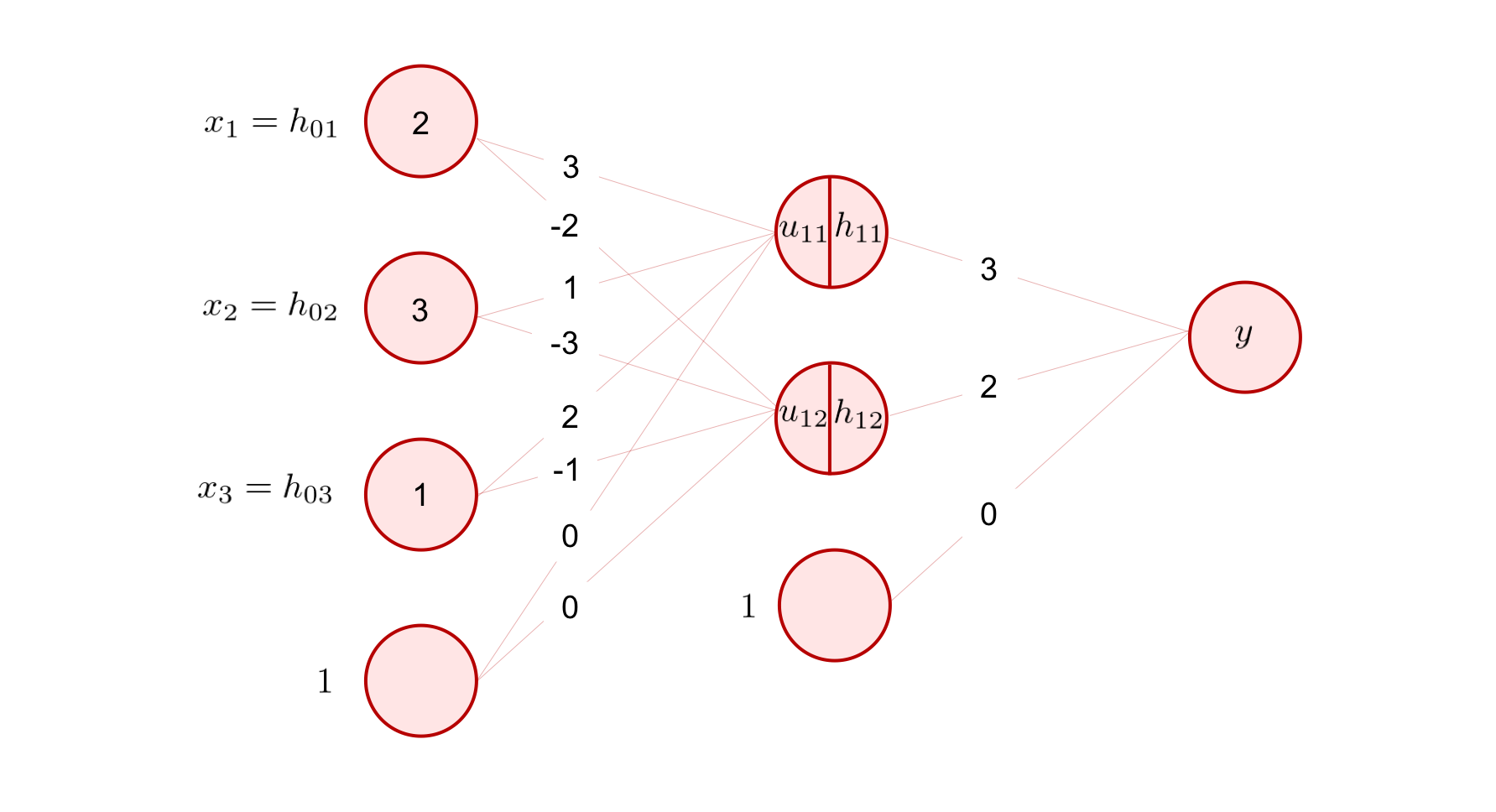
それでは、上の図のような回帰問題を解く 3 層の全結合型ニューラルネットワークを考えて、入力が与えられてから出力が得られるまでの一連の計算を、実際に数値を手計算しながら確認してみましょう。
入力として、
が与えられたとします。 このとき、出力 \(y\) はどのように計算されるのでしょうか。
まず、重み行列 \({\bf W}_{10}\) とバイアスベクトル \({\bf b}_1\) が、図より、以下のような値になっています。
これを用いて、まずは入力に対し線形変換を行います。
次に、非線形変換を施します。 今回は、活性化関数として ReLU 関数を採用しましょう。 活性化関数は、ベクトルを受け取ったとしても基本的には要素ごとに適用されます。
同様に、出力層の \(y\) の値までを計算します。2 層目と 3 層目の間の重み行列 \({\bf W}_{21}\) は、出力側の次元が \(1\) なので、
という \(1 \times 2\) 行列です。バイアスベクトル \({\bf b}_2\) は、図から
であることが分かります。 これらを用いて隠れ層の出力値 \({\bf h}_1\) に対して線形変換を行うと、
が求まりました。 ここでは、ニューラルネットワークを用いて回帰問題を解く場合について説明を行うため、最終出力層に活性化関数を用いていません（注釈3）。
ここまでで、ニューラルネットワークの順伝播計算の中身について詳しく見てきました。
このような計算過程は推論 (inference) とも呼ばれ、一般的には訓練が完了したモデルを用いて新しいデータに対して予測を行うことを指します。 今回の例では、すでに \({\bf W}_{10}\) や \({\bf W}_{21}\) といったパラメータの値は与えられており、それを使って入力に対してニューラルネットワークがどのような値を出力するのかを計算しました。
次節では、この \({\bf W}_{10}\) や \({\bf W}_{21}\) といったパラメータを決定するニューラルネットワークの訓練について解説します。
ニューラルネットワークの訓練¶
重回帰分析では、目的関数をモデルのパラメータで微分して出てきた式を \(= 0\) とおいて、実際の数値を使うことなく変数のまま（\({\bf x}\) や \({\bf t}\) と置いたまま）、解（最適なパラメータ）を求めることができました。 このように、変数のままで解を求めることを解析的に解くと言い、その答えのことを解析解 (analytical solution) と呼びます。
しかし、ニューラルネットワークで表現されるような複雑な関数の場合、最適解を解析的に解くことはほとんどの場合困難です。そのため、別の方法を考える必要があります。
解析的に解く方法に対し、計算機を使って繰り返し数値計算を行って解を求めることを数値的に解くといい、求まった解は数値解 (numerical solution) と呼ばれます。
ニューラルネットワークでは、基本的に数値的な手法によって最適なパラメータを求めます。
そして、これから紹介する代表的な数値的解法では、求めたいパラメータの初期値 (initial value) を事前に決めておく必要があります。 なぜなら、この初期値から少しずつ値を更新していき、望ましい解に近づけていくためです。
このような手法は、最適化手法 (optimization method) と呼ばれるものの一種です。
モデルを設計し
目的関数を定め
目的関数を最適化するパラメータを求める
という手順は、単回帰分析と重回帰分析の章でも、繰り返し出てきました。 そして、この手順は機械学習の他の多くの手法でもよく登場します。 本章で扱うニューラルネットワークでも、この手順に従います。
今回は、モデルとしては前節で説明に用いた 3 層のニューラルネットワークを用います。 このため、ステップ 1 はすでに完了しています。 次節からは、ステップ 2 以降を説明していきます。
目的関数¶
ニューラルネットワークの訓練には、微分可能でさえあれば解きたいタスクに合わせて様々な目的関数を利用することができます。 ここでは、
回帰問題でよく用いられる平均二乗誤差 (mean squared error)
分類問題でよく用いられる交差エントロピー (cross entropy)
という代表的な 2 つの目的関数を紹介します。
平均二乗誤差¶
平均二乗誤差 (mean squared error) は、回帰問題を解きたい場合によく用いられる目的関数です。 重回帰分析の解説中に紹介した二乗和誤差と似ていますが、各データ点における誤差の総和をとるだけでなく、それをデータ数で割って、誤差の平均値を計算している点が異なります。式で表すと、以下のようになります。
ここで、\(N\) はサンプルサイズ、\(y_n\) は \(n\) 個目のデータに対するニューラルネットワークの出力値、\(t_n\) は \(n\) 個目のデータに対する望ましい正解の値です。
ここで、下の図のような例を考えてみましょう。
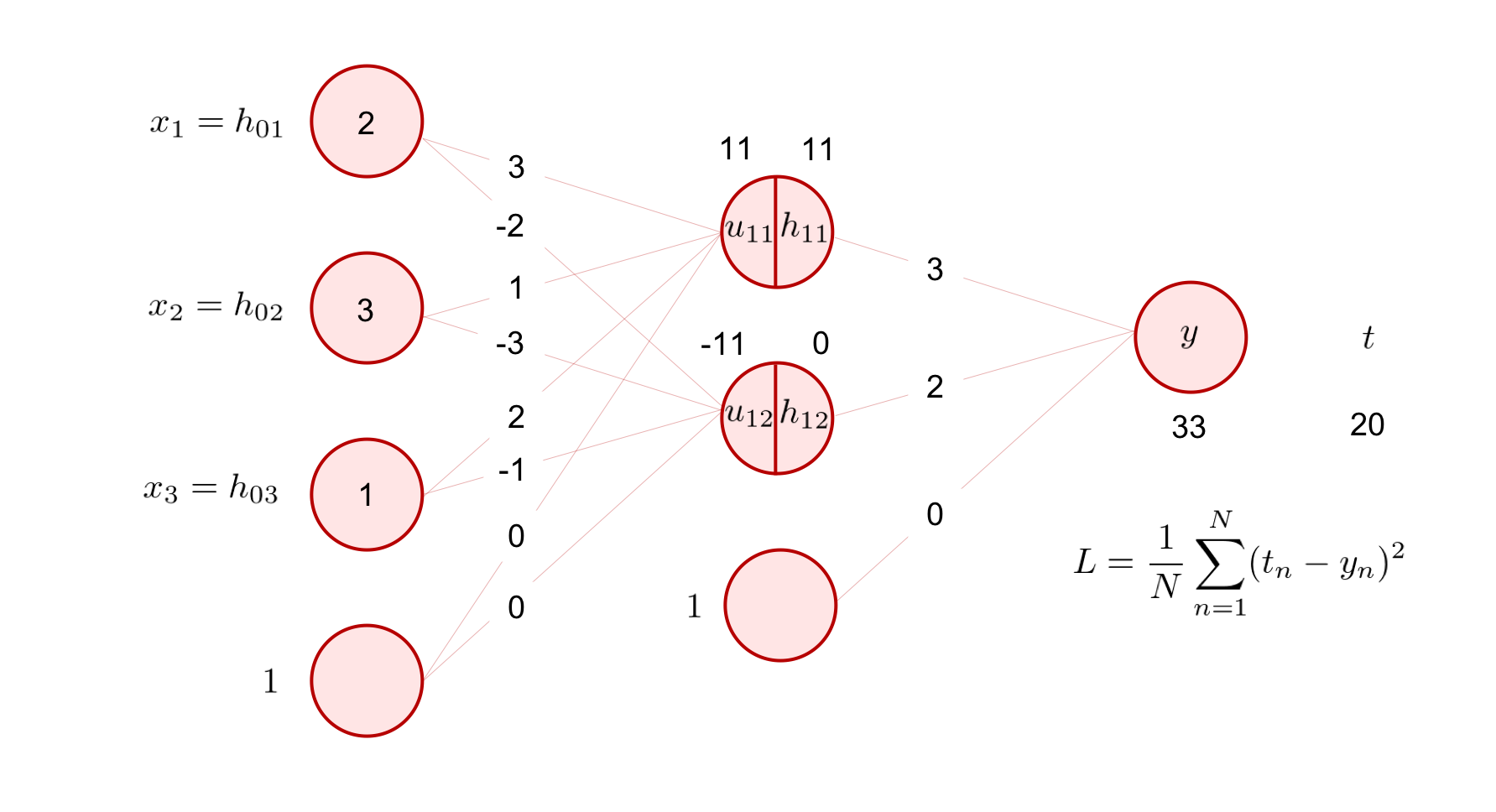
今、ある入力 \({\bf x}\) を与えたときのこのニューラルネットワークの出力 \(y\) は、\(33\) でした。ここで、もしこの入力に対応する目標値が \(t = 20\) だとすると、今全体のサンプルサイズが 1 だとして、平均二乗誤差は
と計算できます。
交差エントロピー¶
交差エントロピー (cross entropy) は、分類問題を解きたい際によく用いられる目的関数です。 例として、\(K\) クラスの分類問題を考えてみましょう。 ある入力 \(x\) が与えられたとき、ニューラルネットワークの出力層に \(K\) 個のノードがあり、それぞれがこの入力が \(k\) 番目のクラスに属する確率
を表しているとします。 これは、入力 \(x\) が与えられたという条件のもとで、予測クラスを意味する \(y\) が \(k\) であるような確率、を表す条件付き確率です。
ここで、\(x\) が所属するクラスの正解が、
というベクトルで与えられているとします。 ただし、このベクトルは \(t_k \ (k=1, 2, \dots, K)\) のいずれか 1 つだけが 1 であり、それ以外は 0 であるようなベクトルであるとします。 これをワンホットベクトル（1-hot vector）と呼びます。 そして、この 1 つだけ値が 1 となっている要素は、その要素のインデックスに対応したクラスが正解であることを意味します。例えば、\(t_3 = 1\) であれば 3 つ目のクラス（3 というインデックスに対応するクラス）が正解であるということになります。
以上を用いて、交差エントロピーは以下のように定義されます。
これは、\(t_k\) が \(k = 1, \dots, K\) のうち正解クラスである一つの \(k\) の値でだけ \(1\) となるので、正解クラスであるような \(k\) での \(\log y_k\) を取り出して \(-1\) を掛けているのと同じです。 また、\(N\) 個すべてのサンプルを考慮すると、交差エントロピーは、
となります。
目的関数の最適化¶
目的関数の値を最小にするようなパラメータの値を求めることで、ニューラルネットワークを訓練します。 本節では、最適化アルゴリズムの一つである勾配降下法 (gradient descent) を紹介します。
勾配降下法¶
図中の点線は、パラメータ \(w\) を変化させた際の目的関数 \(L\) の値を表しています。 この図では簡単のために二次関数で表します。実際のニューラルネットワークの目的関数は、多次元で、かつもっと複雑な形をしていることがほとんどです。 さて、この目的関数が最小値を与えるような \(w\) は、どのようにして求められるのでしょうか。
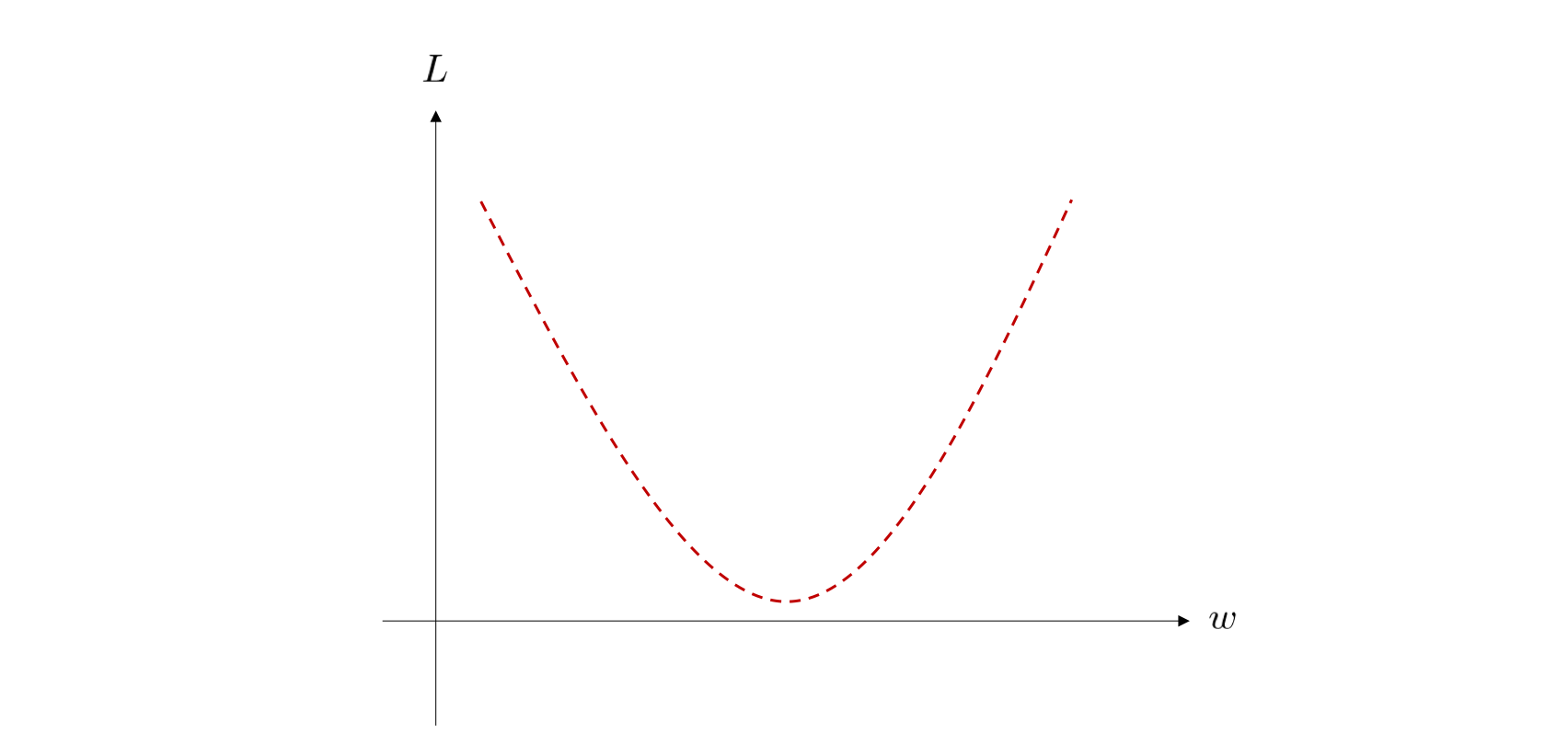
前節で説明したように、ニューラルネットワークのパラメータの初期値を決める必要があります。一般的にニューラルネットワークのパラメータは乱数で初期化されます。 ここでは、例として \(w=4\) という初期化が行われたと考えてみましょう。
そうすると、\(w=4\) における \(L\) の接線の傾き \(\frac{\partial L}{\partial w}\) が求まります。この接線の傾きのことを勾配 (gradient) と一般的に呼びます。
さて、ここでは仮に \(w=4\) における \(\frac{\partial L}{\partial w}\) が \(5\) であったとしましょう。 このことを
と書きます。 この \(5\) という値は \(w=4\) における \(L(w)\) という関数の勾配を表しています。
勾配とは、\(w\) を増加させた際に \(L\) が増加する方向を意味しています。今は \(L\) の値を小さくしたいわけですから、この傾きの逆方向へ \(w\) を変化させる、すなわち \(w\) から \(\frac{\partial L}{\partial w}\) を引けば良い ことになります。
これがニューラルネットワークのパラメータを目的関数の勾配を用いて更新していく際の基本的な考え方です。 このときの \(w\) の一度の更新量の幅を調整するために、勾配に学習率 (learning rate) と呼ばれる値を乗じるのが一般的です。学習率を \(\eta\) とおくと、 \(w\) から \(\eta \frac{\partial L}{\partial w}\) を引くことで、勾配そのものの値を \(\eta\) にした量だけ \(w\) を更新することになります。更新後の \(w\) は、
となります。 ここで、 \(\leftarrow\) は、右側の値で左側の値を置き換える、つまり更新することを意味しています。
例えば、学習率を \(\eta = 0.5\) に設定して、更新後の \(w\) を実際に求めてみましょう。 \(w\) の更新量は学習率 \(\times\) 勾配で決まるので、
となります。 現在 \(w=4\) なので、この値を引いて
と更新した後は、 \(w=1.5\) です。
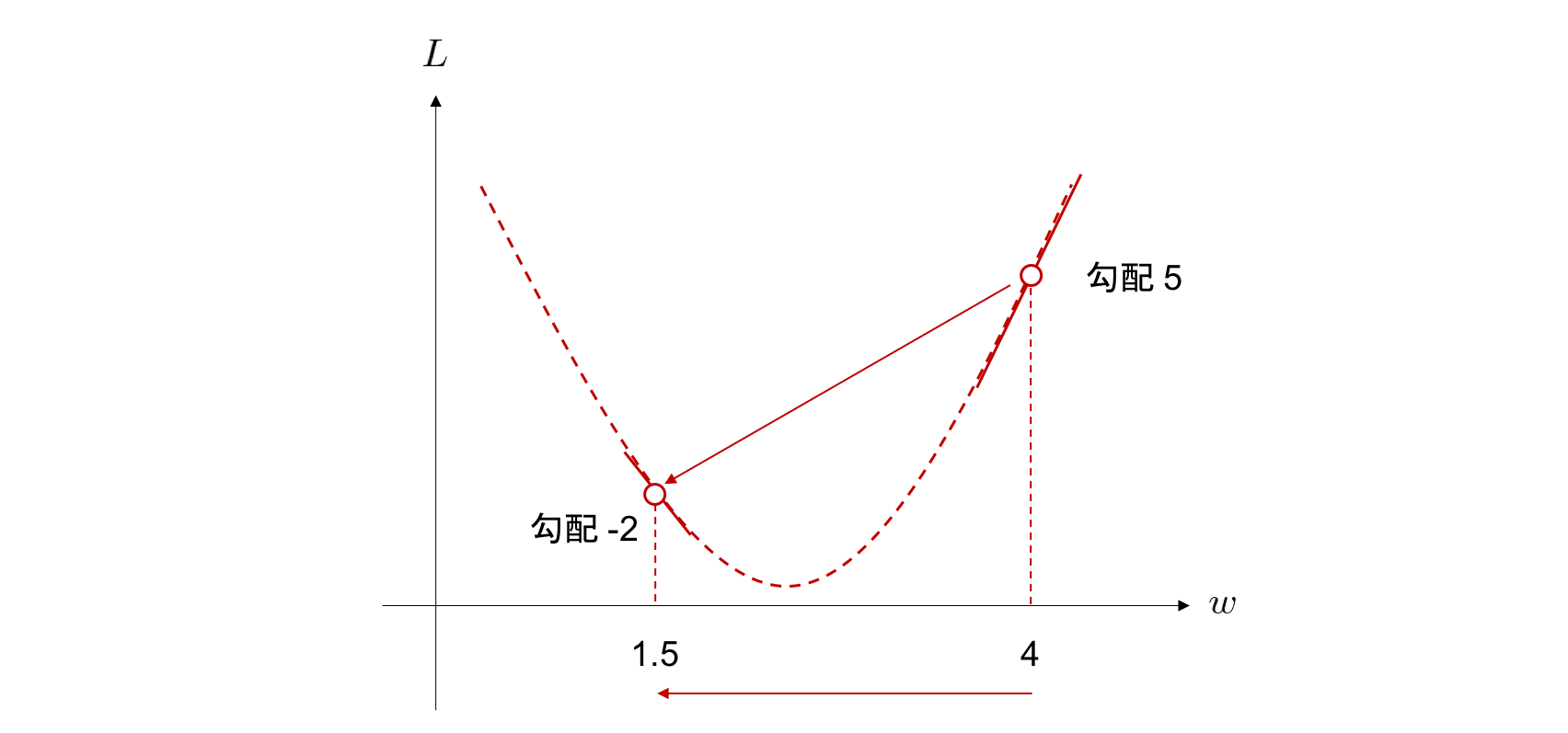
1 度目の更新を行って、\(w\) が \(w = 1.5\) の位置に移動しました。 そこで、再度この点においても勾配を求めてみます。 今度は勾配が \(-2\) になっていたとしましょう。 すると学習率 \(\times\) 勾配は
となります。 これを再び用いて、
と 2 度目の更新を行うと、今度は \(w = 2.5\) の位置にきます。 このようにして 2 回更新したあとは、以下の図の位置にパラメータが移動しています。
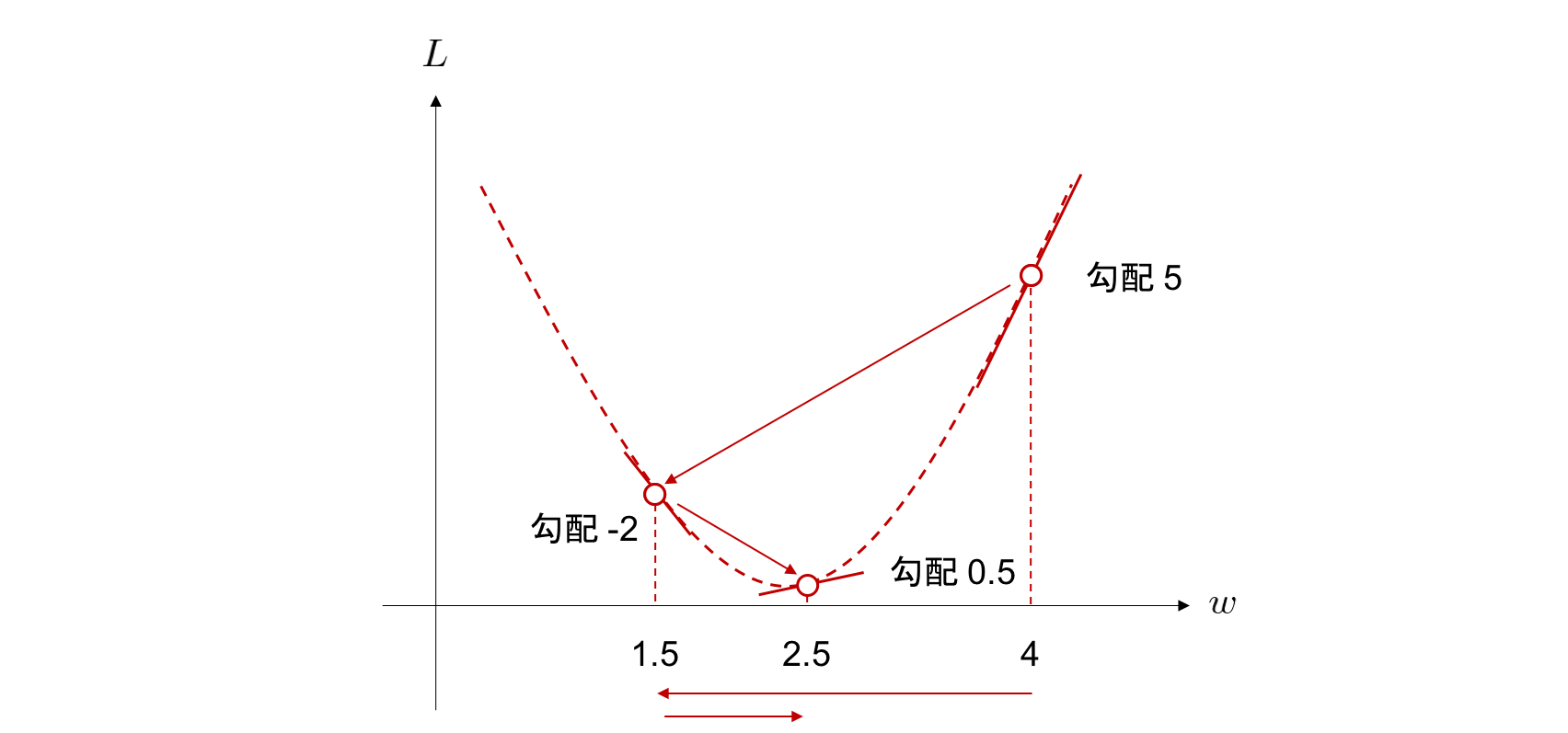
徐々に \(L\) が最小値をとるときの \(w\) の値に近づいていることが見て取れます。
こうして、学習率 \(\times\) 勾配を更新量としてパラメータを変化させていくと、パラメータ \(w\) を求めたい \(L\) を最小にする \(w\) に徐々に近づけていくことができます。
このような勾配を用いた目的関数の最適化手法を勾配降下法 (gradient descent) と呼びます。 ニューラルネットワークは、基本的に微分可能な関数のみをつなげ合わせてできている（注釈4）ため、ニューラルネットワーク全体が表す関数も微分可能であり、訓練データセットを用いて勾配降下法によって目的関数を小さくする（局所）最適なパラメータを求めることができます。
ミニバッチ学習¶
通常ニューラルネットワークを勾配降下法で最適化する場合は、データを一つ一つ用いてパラメータを更新するのではなく、いくつかのデータをまとめて入力し、それぞれの勾配を計算したあと、その勾配の平均値を用いてパラメータの更新を行う方法がよく行われます。 これをミニバッチ学習と呼びます。
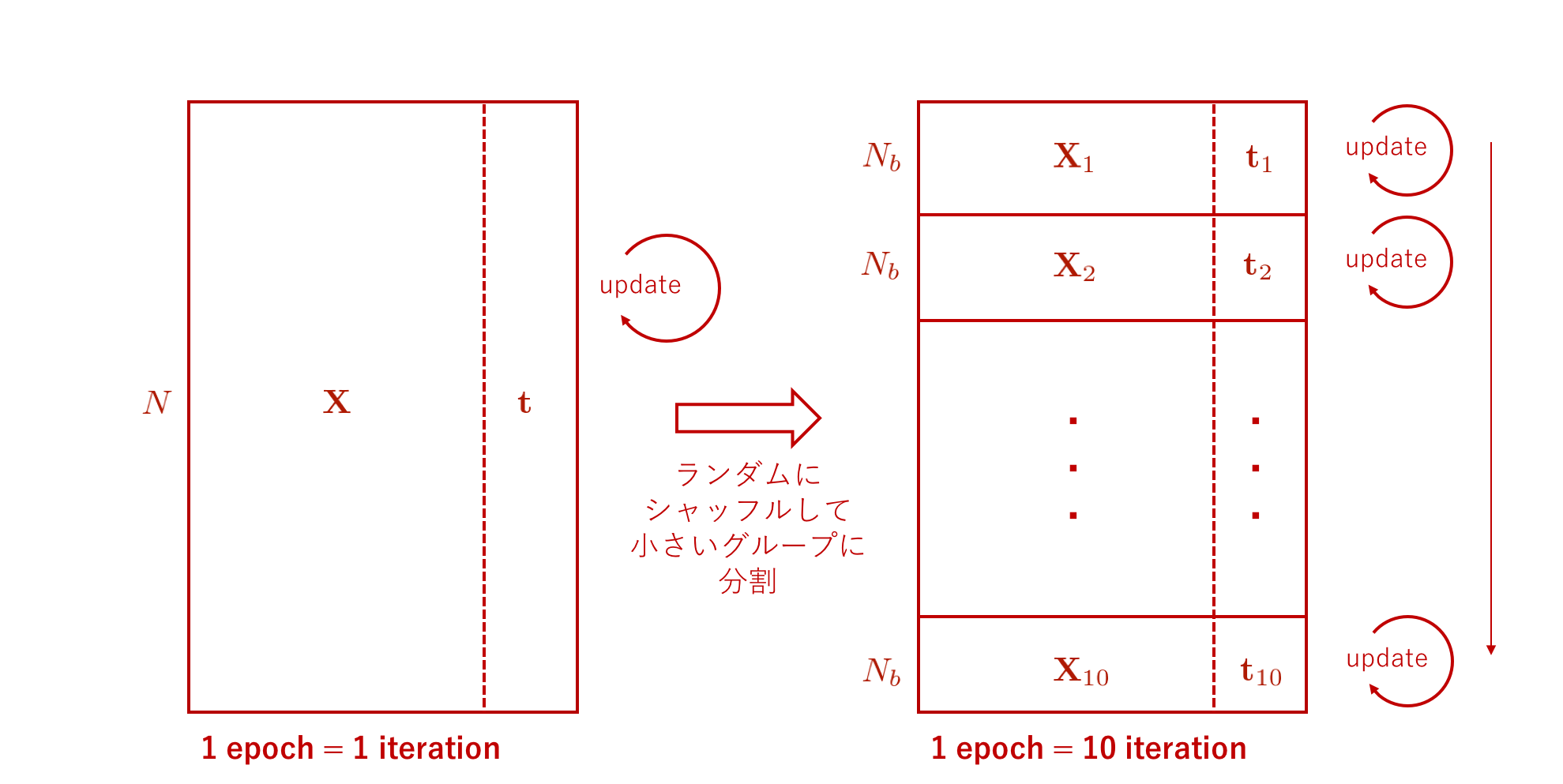
ミニバッチ学習では、以下の手順で訓練を行います。
訓練データセットから一様ランダムに \(N_{b} \ (>0)\) 個のデータを抽出する
その \(N_{b}\) 個のデータをまとめてニューラルネットワークに入力し、それぞれのデータに対する目的関数の値を計算する
\(N_b\) 個の目的関数の値の平均をとる
この平均の値に対する各パラメータの勾配を求める
求めた勾配を使ってパラメータを更新する
そしてこれを、異なる \(N_{b}\) 個のデータの組み合わせに対して繰り返し行います。
ここで、一度のパラメータ更新に用いられるサンプルの数 \(N_{b}\) をバッチサイズ (batch size) と呼びます。 結果的にはデータセットに含まれる全てのデータを使用していきますが、1 度の更新に用いるデータは \(N_{b}\) 個ずつであることに注意してください。
データセットから \(N_b\) 個ずつデータを取ってきて使うというミニバッチ学習の様子を模式的に表した図を上に示します。この図では、データセットをそれぞれが \(N_b\) 個ずつデータを含んでいる 10 個のグループに分割しています。そのあと、それぞれのグループごとにパラメータ更新を逐次的に行います。
ミニバッチ学習と異なり、データセット全体を一度に用いて一回の更新を行う、すなわちグループへ分割しない方法をバッチ学習と呼びます。
勾配降下法では、データを用いてパラメータを 1 度更新するまでのことを 1 イテレーション (iteration) と呼び、バッチ学習では訓練データセットのデータ全体を 1 度の更新に一気に用いるため、1 エポック = 1 イテレーション となります。 一方、例えばデータセットを 10 個のグループに分割してグループごとに更新を行うミニバッチ学習の場合は、1 エポック = 10 イテレーション となります。
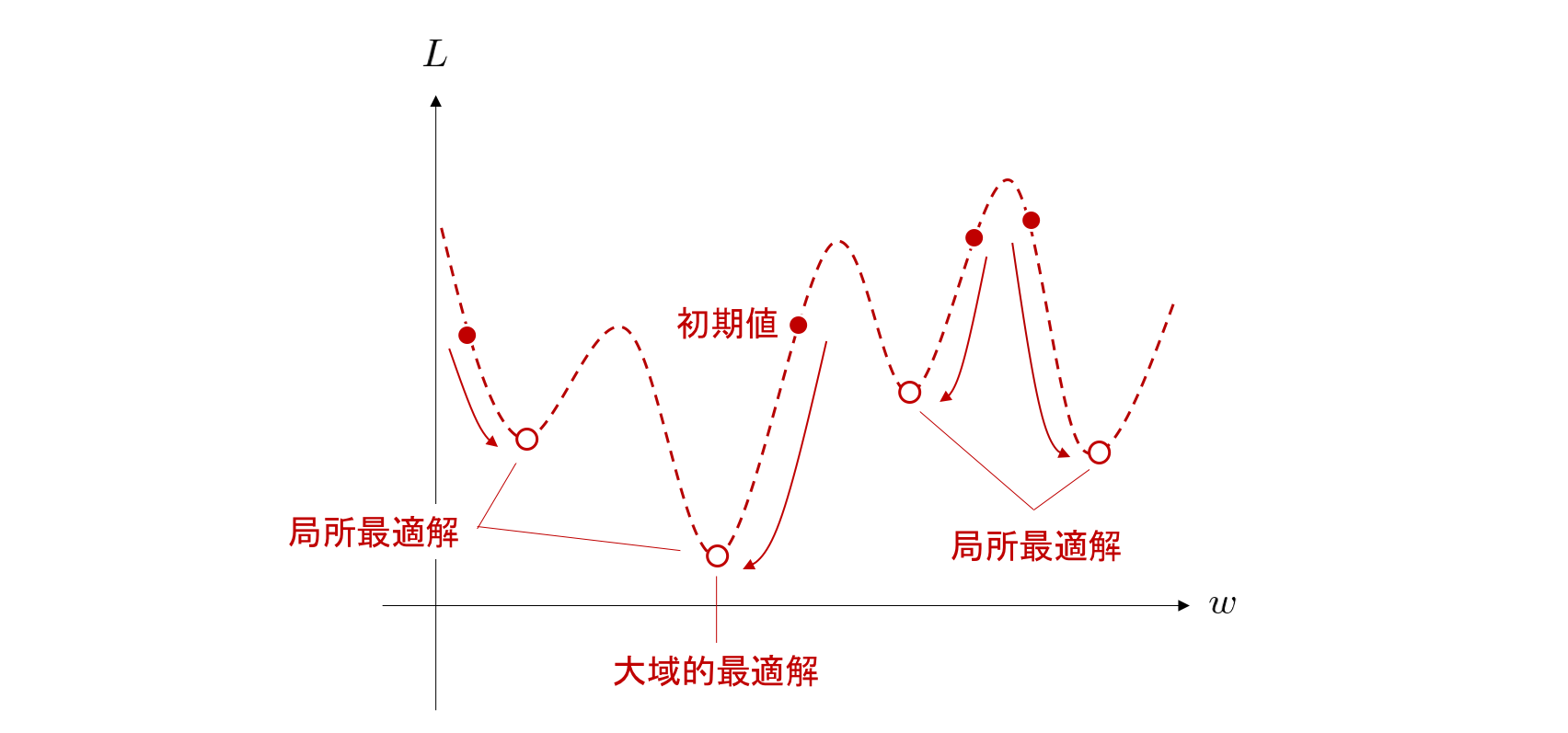
このようなミニバッチ学習を用いた勾配降下法は特に、確率的勾配降下法（stocastic gradient descent; SGD）と呼ばれます。 現在多くのニューラルネットワークの最適化手法はこの SGD をベースとした手法となっています。 SGD を用いると、全体の計算時間が劇的に少なくできるだけでなく、下図のように目的関数が複数の谷を持っていたとしても、適当な条件のもとで 「ほとんど確実に」 局所最適解（注釈5）に収束することが知られています。
パラメータ更新量の算出¶
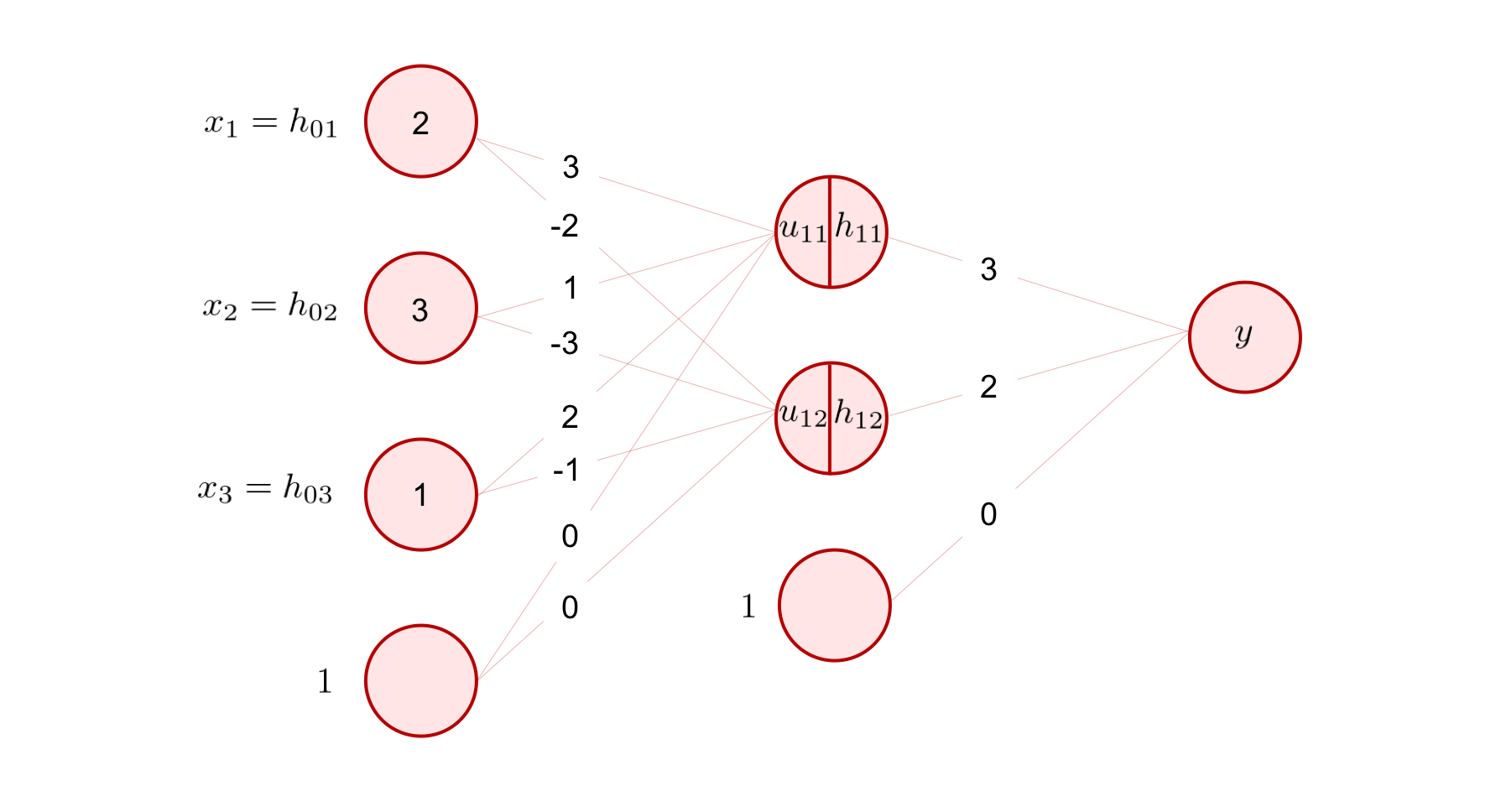
それでは今、下図のような3層の全結合型ニューラルネットワークを考え、3 次元の入力ベクトルから、1 次元の値を出力し、正解の値を予測する回帰問題を題材に、パラメータを更新する式の導入を行ってみましょう。
まず、1 層目と 2 層目の間の線形変換が \({\bf w}_1, {\bf b}_1\)、2 層目と 3 層目の間の線形変換が \({\bf w}_2, {\bf b}_2\) というパラメータによって表されているとします。 また、これらをまとめて \(\boldsymbol{\Theta}\) と表すことにします。つまり、\(\boldsymbol{\Theta} = \{ {\bf w}_1, {\bf b}_1, {\bf w}_2, {\bf b}_2 \}\) です（注釈6）。
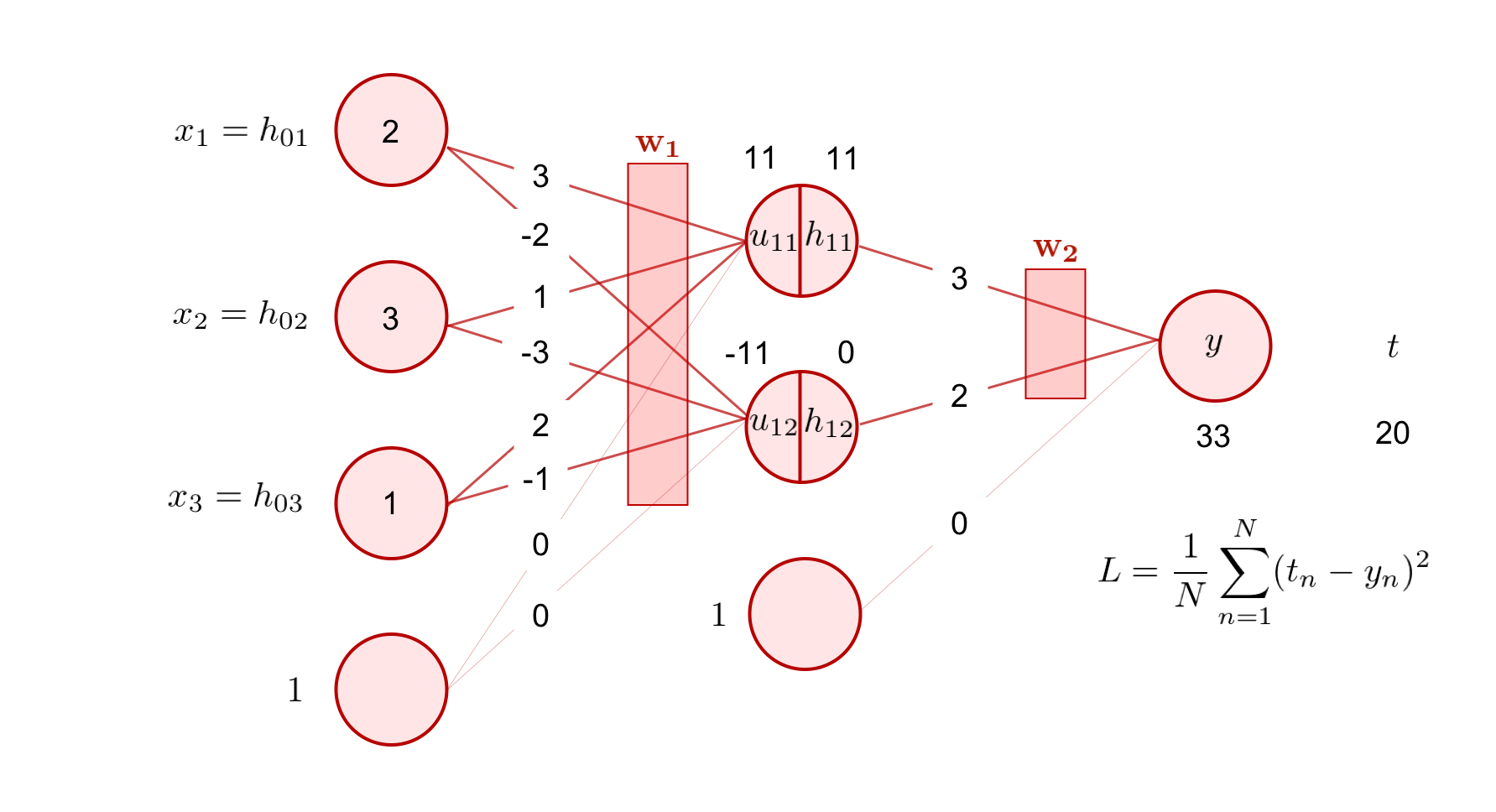
入力は \({\bf x} \in \mathbb{R}^{3}\)、出力を \(y\) とし、目標値を \(t\) とおきます。目的関数には以下の平均二乗誤差関数を用いることにします。
ただし、\(N\) はデータ数です。 今回は \(N=1\) なので、目的関数は簡単に
と書けます。
それでは、この目的関数を各パラメータで微分して、それぞれのパラメータについて更新量を算出してみましょう。
まず、順伝播を計算します。 ニューラルネットワーク全体を一つの関数として見て \(f\) と書くことにすると、出力 \(y\) は
と書くことができます。ここで、\(a_1\) は 1 層目のノードで行われる非線形変換（に使用される活性化関数）を意味しています。今回は、シグモイド関数をこの活性化関数に用いることにします。
以下、簡単のために、入力に対して行われた線形変換の結果を \({\bf u}_1\) とし、中間層の値、すなわち \({\bf u}_1\) に活性化関数を適用した結果を \({\bf h}_1\) と書きます。 すると、これらの関係は以下のように整理することができます。
パラメータ \({\bf w}_2\) の更新量¶
それではまず、出力層に近い方のパラメータ、\({\bf w}_2\) についての \(L\) の勾配を求めてみましょう。 これは、合成関数の偏微分なので、連鎖律（chain rule）を用いて以下のように展開できます。
2 つの偏微分の積が現れました。 これらはそれぞれ、
と求まります。
それでは、実際に NumPy を使ってこの勾配の値を計算してみましょう。 ここでは簡単のために、バイアスベクトルはすべて 0 で初期化されているとします。
[1]:
import numpy as np
# 入力
x = np.array([2, 3, 1])
# 正解
t = np.array([20])
まず、NumPy モジュールを読み込んでから、入力の配列を定義します。 ここでは、上図と同じになるように 2, 3, 1 の3つの値を持つ3次元ベクトルを定義しています。 また、正解として図と同じように 20 を与えることにしました。 次に、パラメータを定義します。
[2]:
# 0-1層間のパラメータ
w1 = np.array([[3, 1, 2], [-2, -3, -1]])
b1 = np.array([0, 0])
# 2-3層間のパラメータ
w2 = np.array([[3, 2]])
b2 = np.array([0])
ここでは、以下の4つのパラメータを定義しました。
1 層目と 2 層目の間の線形変換のパラメータ
\({\bf w}_1 \in \mathbb{R}^{2 \times 3}\) : 3 次元ベクトルを 2 次元ベクトルに変換する行列
\({\bf b}_1 \in \mathbb{R}^2\) : 2 次元バイアスベクトル
2 層目と 3 層目の間の線形変換のパラメータ
\({\bf w}_2 \in \mathbb{R}^{1 \times 2}\) : 2 次元ベクトルを 1 次元ベクトルに変換する行列
\({\bf b}_2 \in \mathbb{R}^1\) : 1 次元バイアスベクトル
それでは、各層の計算を実際に実行してみましょう。
[3]:
# 中間層の計算
u1 = w1.dot(x) + b1
h1 = 1. / (1 + np.exp(-u1))
# 出力の計算
y = w2.dot(h1) + b2
print(y)
[2.99995156]
出力は \(2.99995156\) と求まりました。 つまり、\(f([2, 3, 1]^T) = 2.99995156\) ということになります。 次に、上で導出した
の右辺の 2 つの偏微分をそれぞれ計算してみましょう。
[4]:
# dL / dy
dLdy = -2 * (t - y)
# dy / dw_2
dydw2 = h1
これらを掛け合わせれば、求めたかったパラメータ \({\bf w}_2\) についての勾配を得ることができます。
[5]:
# dL / dw_2: 求めたい勾配
dLdw2 = dLdy * dydw2
print(dLdw2)
[-3.39995290e+01 -2.82720335e-05]
勾配が求まりました。 これが \(\frac{\partial L}{\partial {\bf w}_2}\) の値です（注釈7）。 これを学習率でスケールさせたものを使えば、パラメータ \({\bf w}_2\) を更新することができます。 更新式は、具体的には以下のようになります。
学習率について¶
学習率が大きすぎると、繰り返しパラメータ更新を行っていく中で目的関数の値が振動したり、発散したりしてしまいます。 逆に小さすぎると、収束に時間がかかってしまいます。 そのため、この学習率を適切に決定することがニューラルネットワークの学習においては非常に重要となります。 多くの場合、学習がきちんと進むもっとも大きな値を経験的に探すということが行われます。 シンプルな画像認識のタスクなどでは大抵、\(0.1\) から \(0.01\) 程度の値が最初に試される場合が比較的多く見られます。
パラメータ \({\bf w}_1\) の更新量¶
次に、\({\bf w}_1\) の更新量も求めてみましょう。 そのためには、\({\bf w}_1\) で目的関数 \(L\) を偏微分した値が必要です。 これは以下のように計算できます。
4 つの偏微分の積になりました。 ここで、活性化関数の勾配
が登場しています。 今回は活性化関数 \(a_1\) にシグモイド関数を用いているので、
を \({\bf u}_1\) で微分します。
このように、シグモイド関数の勾配は、シグモイド関数の出力値を使って簡単に計算することができます。
これで、上の 4 つの偏微分のうち、初めの 1 つと、3 つ目はすでに求めました。 残りの 2 つは、それぞれ、
と計算できます。 では、さっそく実際に NumPy を用いて計算を実行してみましょう。
[6]:
# d y / d h1
dydh1 = w2
# d h1 / d u1
dh1du1 = h1 * (1 - h1)
# d u_1 / d w1
du1dw1 = x
# 上から du1 / dw1 の直前までを一旦計算
dLdu1 = dLdy * dydh1 * dh1du1
# du1dw1は (3,) というshapeなので、g_u1w1[None]として(1, 3)に変形
du1dw1 = du1dw1[None]
# dL / dw_1: 求めたい勾配
dLdw1 = dLdu1.T.dot(du1dw1)
print(dLdw1)
[[-3.40704286e-03 -5.11056429e-03 -1.70352143e-03]
[-1.13088040e-04 -1.69632060e-04 -5.65440200e-05]]
これが \(\frac{\partial L}{\partial {\bf w}_1}\) の値です（注釈7）。 これを用いて、\({\bf w}_2\) と同様に以下のような更新式でパラメータ \({\bf w}_1\) の更新をすることができます。
これで \({\bf w}_1\) の更新をすることができました。 \({\bf b}_1\) 、\({\bf b}_2\) についても同様の流れで更新することができます。
誤差逆伝播法（バックプロパゲーション）¶
ここまでで、各パラメータについての目的関数の導関数を手計算により導出して実際に勾配の数値計算を行うということを体験しました。 では、もっと層数の多いニューラルネットワークの場合は、どうなるでしょうか。
同様に手計算によって全てのパラメータの勾配を求めることも不可能ではないかもませんが、層数が多くなれば膨大な時間がかかるでしょう。しかし、ニューラルネットワークの微分可能な関数を順に適用するという性質を用いると、コンピュータによって自動的に勾配を与える関数を導き出すことが可能です。
まず、合成関数の偏微分は、連鎖律によって複数の偏微分の積の形に変形できることを思い出しましょう。
下図は、ここまでの説明で用いていた 3 層の全結合型ニューラルネットワークの出力を得るための計算（順伝播）と、その値を使って目的関数の値を計算する過程を青い矢印で、そして前節で手計算によって行った各パラメータによる目的関数の偏微分を計算する過程を赤い矢印で表現した動画となっています。
まず、目的関数の出力を \(l = L(y, t)\) とします。 この図の丸いノードは変数を表し、四角いノードは関数を表しています。
今、一つの巨大な合成関数として見たニューラルネットワーク全体を \(f\) と表し、その中で各層間の線形変換に用いられる関数を \(f_1\), \(f_2\)、中間層での非線形変換を \(a_1\) と表します。
今、上図の青い矢印で表されるように、新しい入力 \({\bf x}\) がニューラルネットワークに与えられ、それが順々に出力側に伝わっていき、最終的に目的関数の値 \(l\) まで計算が終わったとします。
すると次は、目的関数の出力の値を小さくするような各パラメータの更新量を求めたいということになりますが、このために必要な目的関数の勾配は、各パラメータの丸いノードより先の部分（出力側）にある関数の勾配だけで計算できることが分かります。 具体的には、それらを全て掛け合わせたものになっています。
つまり、上図の赤い矢印で表されるように、出力側から入力側に向かって、順伝播とは逆向きに、各関数における入力についての勾配を求めて、掛け合わせていけば、パラメータについての目的関数の勾配が計算できるわけです。
このように、微分の連鎖律の仕組みを用いて、ニューラルネットワークを構成する関数が持つパラメータについての目的関数の勾配を、順伝播で通った経路を逆向きにたどるようにして途中の関数の勾配の掛け算によって求めるアルゴリズムを 誤差逆伝播法 (backpropagation) と呼びます。
勾配消失¶
活性化関数について初めに触れた際、シグモイド関数には勾配消失という現象が起きやすくなるという問題があり、現在はあまり使われていないと説明をしました。 その理由についてもう少し詳しく見ていきましょう。
上で既に計算した、シグモイド関数の導関数を思い出してみます。
さて、この導関数の値を入力変数に関してプロットしてみると、下記のようになります。
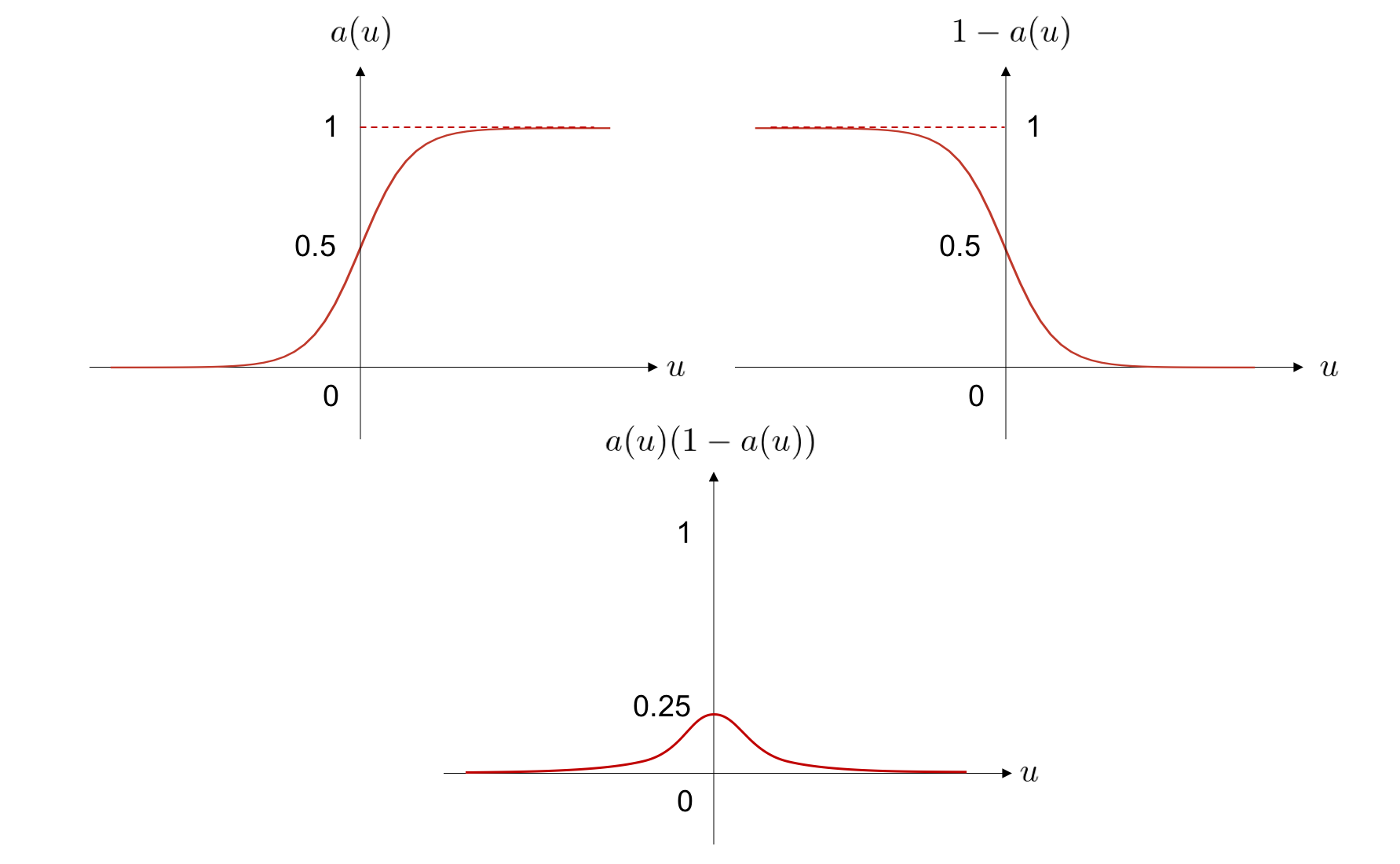
この図の上 2 つは、導関数を構成する2つの部分、 \(f(u)\) および \(1 - f(u)\) の値を別々にプロットしたもので、中央下の図は全体の導関数の値となります。 中央下の導関数の形から明らかなように、入力が原点から遠くなるにつれ勾配の値がどんどん小さくなり、0に漸近していくことが分かります。
各パラメータの更新量を求めるには、前節で説明したように、そのパラメータよりも先のすべての関数の勾配を掛け合わせる必要がありました。 このとき、活性化関数にシグモイド関数を用いていると、勾配は必ず最大でも 0.25 という値にしかなりません。 つまり、シグモイド関数がニューラルネットワーク中に現れるたびに、目的関数の勾配は、多くとも 0.25 倍されてしまいます。 これは、層数が増えていけばいくほど、この最大でも 0.25 にしかならないような値が、繰り返し掛け合わされることになってしまい、入力に近い層に流れていく勾配はどんどん 0 に近づいていってしまいます。
具体例を見てみましょう。 今回は 3 層のニューラルネットワークを用いて説明を行っていましたが、4層の場合を考えてみます。 すると、一番入力に近い線形変換のパラメータの勾配は、多くとも目的関数の勾配を \(0.25 \times 0.25 = 0.0625\) 倍したものということになります。 層数が一つ増えるたびに、指数的に勾配が小さくなるということがよく分かります。
ディープラーニングでは、4 層よりもさらに多くの層を積み重ねたニューラルネットワークが用いられます。 そうすると、活性化関数としてシグモイド関数を使用した場合、目的関数の勾配が入力に近い関数が持つパラメータへほぼ全く伝わらなくなってしまいます。 あまりにも小さな勾配しか伝わってこなくなると、パラメータの更新量がほとんど 0 になるため、どんなに目的関数が大きな値になっていても、入力層に近い関数が持つパラメータは変化しなくなります。 つまり初期化時からほとんど値が変わらなくなるということになり、学習が行われていないという状態になるわけです。 これを勾配消失と呼び、長らく深い（十数層を超える）ニューラルネットワークの学習が困難であった一つの要因でした。
この解決策として、ReLU 関数が提案され、多層のニューラルネットワークに対する学習も勾配消失を回避しながら行うことができるようになっています。
注釈 1
通常、数学では線形変換とは \({\bf W}\) を掛ける操作のことを指し、\({\bf b}\) を足す操作は含まれません。\({\bf b}\) の加算を含む操作は厳密には「アファイン変換（もしくは アフィン変換）」と呼ばれるものです。しかし、ディープラーニングの文脈ではこの変換も線形変換と呼ばれることが多いです。
注釈 2
ここで、入力層のノードが \(h_{01}, h_{02}, h_{03}\) という文字で表されていますが、この \(h\) は隠れ層を意味する英語の hidden layer の頭文字である h から来ています。 入力層は隠れ層ではありませんが、同じ文字を使うことで表記を一般化し、簡便にしています。
注釈 3
また、分類問題を解きたい場合は、クラス数と同じだけのノードを出力層に用意しておき、各ノードがあるクラスに入力が属する確率を表すようにします。 このため、全出力ノードの値の合計が 1 になるよう正規化します。 これには、要素ごとに適用される活性化関数ではなく、層ごとに活性値を計算する別の関数を用いる必要があります。 そのような目的に使用される代表的な関数には、ソフトマックス関数があります。
注釈 4
厳密には目的関数に微分不可能な点が存在する可能性はあります。例えば ReLU は \(x = 0\) で微分不可能なため、ReLU を含んだニューラルネットワークには微分不可能な点が存在することになります。このような場合、劣微分（subderivative, subdifferential）という考え方を導入し、全ての点で勾配が決定できるようにすることなどが行われます。
注釈 5
この局所解が大域的最適解と一致する条件については、現在活発に研究が行われています。参考：」A Convergence Theory for Deep Learning via Over-Parameterization」
[7]:
import chainer
import chainer.functions as F
import chainer.links as L
# 1-2層間のパラメータ
w1 = np.array([[3, 1, 2], [-2, -3, -1]], dtype=np.float32)
b1 = np.array([0, 0], dtype=np.float32)
l1 = L.Linear(2, initialW=w1, initial_bias=b1)
# 2-3層間のパラメータ
w2 = np.array([[3, 2]], dtype=np.float32)
b2 = np.array([0], dtype=np.float32)
l2 = L.Linear(1, initialW=w2, initial_bias=b2)
# 入力
x = np.array([[2, 3, 1]], dtype=np.float32)
# 出力
y = l2(F.sigmoid(l1(x)))
print(y) # => should be [2.99995156]
# 正解
t = np.array([[20.]], dtype=np.float32)
# ロス
loss = F.mean_squared_error(y, t)
# dLdw_2
print(chainer.grad([loss], [l2.W])) # => should be [-3.39995290e+01 -2.82720335e-05]
# dLdw_1
print(chainer.grad([loss], [l1.W])) # => should be [[-3.40704286e-03 -5.11056429e-03 -1.70352143e-03]
# [-1.13088040e-04 -1.69632060e-04 -5.65440200e-05]]
variable([[2.9999516]])
[variable([[-3.3999527e+01, -2.8371891e-05]])]
[variable([[-3.4045703e-03, -5.1068552e-03, -1.7022851e-03],
[-1.1348747e-04, -1.7023120e-04, -5.6743735e-05]])]